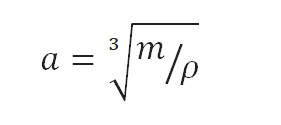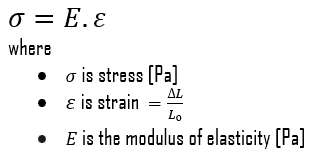Bronce de aluminio – Densidad – Resistencia – Dureza – Punto de fusión

Acerca del bronce de aluminio

Los bronces de aluminio son una familia de aleaciones a base de cobre que ofrecen una combinación de propiedades mecánicas y químicas incomparables con cualquier otra serie de aleaciones. Contienen entre un 5 y un 12% de aluminio. Además, los bronces de aluminio también contienen níquel, silicio, manganeso y hierro. Tienen una resistencia excelente, similar a la de los aceros de baja aleación, y una excelente resistencia a la corrosión, especialmente en agua de mar y entornos similares, donde las aleaciones a menudo superan a muchos aceros inoxidables. Su excelente resistencia a la corrosión se debe al aluminio de las aleaciones, que reacciona con el oxígeno atmosférico para formar una capa superficial delgada y resistente de alúmina (óxido de aluminio) que actúa como barrera a la corrosión de la aleación rica en cobre. Se encuentran en forma forjada y fundida. Los bronces de aluminio suelen ser de color dorado.

Resumen

Nombre	Bronce de aluminio
Fase en STP	sólido
Densidad	7640 kg / m3
Resistencia a la tracción	550 MPa
Límite de elastacidad	250 MPa
Módulo de Young	110 GPa
Dureza Brinell	170 BHN
Punto de fusion	1030 ° C
Conductividad térmica	59 W / mK
Capacidad calorífica	380 J / g K
Precio	9 $ / kg

Densidad del bronce de aluminio

Las densidades típicas de varias sustancias se encuentran a presión atmosférica. La densidad  se define como la  masa por unidad de volumen . Es una  propiedad intensiva , que se define matemáticamente como masa dividida por volumen:  ρ = m / V

En palabras, la densidad (ρ) de una sustancia es la masa total (m) de esa sustancia dividida por el volumen total (V) ocupado por esa sustancia. La unidad estándar del SI es  kilogramos por metro cúbico  ( kg / m ³ ). La unidad de inglés estándar es  libras de masa por pie cúbico  ( lbm / ft ³ ).

La densidad del bronce de aluminio es 7640 kg / m ³ .

Ejemplo: densidad

Calcula la altura de un cubo hecho de bronce de aluminio, que pesa una tonelada métrica.

Solución:

La densidad  se define como la  masa por unidad de volumen . Se define matemáticamente como masa dividida por volumen:

ρ = m / V

Como el volumen de un cubo es la tercera potencia de sus lados (V = a ³ ), la altura de este cubo se puede calcular:

La altura de este cubo es entonces a = 0,508 m .

Propiedades mecánicas del bronce de aluminio

Los materiales se eligen con frecuencia para diversas aplicaciones porque tienen combinaciones deseables de características mecánicas. Para aplicaciones estructurales, las propiedades de los materiales son cruciales y los ingenieros deben tenerlas en cuenta.

Resistencia del bronce de aluminio

En mecánica de materiales, la resistencia de un material es su capacidad para soportar una carga aplicada sin fallas ni deformaciones plásticas. La resistencia de los materiales básicamente considera la relación entre las cargas externas aplicadas a un material y la deformación resultante o cambio en las dimensiones del material. La resistencia de un material es su capacidad para soportar esta carga aplicada sin fallas ni deformaciones plásticas.

Resistencia a la tracción

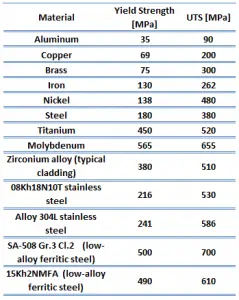
La máxima resistencia a la tracción del bronce de aluminio: UNS C95400 es de aproximadamente 550 MPa.

La máxima resistencia a la tracción es la máxima en la curva de ingeniería de tensión-deformación . Esto corresponde a la tensión máximaque puede ser sostenido por una estructura en tensión. La resistencia máxima a la tracción a menudo se reduce a «resistencia a la tracción» o incluso a «máxima». Si se aplica y se mantiene esta tensión, se producirá una fractura. A menudo, este valor es significativamente mayor que el límite elástico (entre un 50 y un 60 por ciento más que el rendimiento para algunos tipos de metales). Cuando un material dúctil alcanza su máxima resistencia, experimenta un estrechamiento donde el área de la sección transversal se reduce localmente. La curva de tensión-deformación no contiene una tensión mayor que la resistencia máxima. Aunque las deformaciones pueden seguir aumentando, la tensión suele disminuir después de que se ha alcanzado la resistencia máxima. Es una propiedad intensiva; por lo tanto, su valor no depende del tamaño de la muestra de prueba. Sin embargo, depende de otros factores, como la preparación de la muestra,temperatura del entorno de prueba y del material. Las resistencias a la tracción máxima varían desde 50 MPa para un aluminio hasta 3000 MPa para aceros de muy alta resistencia.

Límite de elastacidad

El límite elástico del bronce de aluminio – UNS C95400 es de aproximadamente 250 MPa.

El punto de fluencia es el punto en una curva de tensión-deformación que indica el límite del comportamiento elástico y el comportamiento plástico inicial. Fuerza de produccióno el límite elástico es la propiedad del material definida como el esfuerzo en el que un material comienza a deformarse plásticamente, mientras que el límite elástico es el punto donde comienza la deformación no lineal (elástica + plástica). Antes del límite elástico, el material se deformará elásticamente y volverá a su forma original cuando se elimine la tensión aplicada. Una vez que se supera el límite de fluencia, una fracción de la deformación será permanente e irreversible. Algunos aceros y otros materiales exhiben un comportamiento denominado fenómeno de límite elástico. Los límites de elasticidad varían de 35 MPa para un aluminio de baja resistencia a más de 1400 MPa para aceros de muy alta resistencia.

Módulo de Young

El módulo de Young del bronce de aluminio – UNS C95400 es de aproximadamente 110 GPa.

El módulo de Young es el módulo elástico para esfuerzos de tracción y compresión en el régimen de elasticidad lineal de una deformación uniaxial y generalmente se evalúa mediante ensayos de tracción. Hasta una tensión límite, un cuerpo podrá recuperar sus dimensiones al retirar la carga. Las tensiones aplicadas hacen que los átomos de un cristal se muevan desde su posición de equilibrio. Todos los átomos se desplazan en la misma cantidad y aún mantienen su geometría relativa. Cuando se eliminan las tensiones, todos los átomos vuelven a sus posiciones originales y no se produce ninguna deformación permanente. Según la ley de Hooke , la tensión es proporcional a la deformación (en la región elástica) y la pendiente es el módulo de Young.. El módulo de Young es igual a la tensión longitudinal dividida por la deformación.

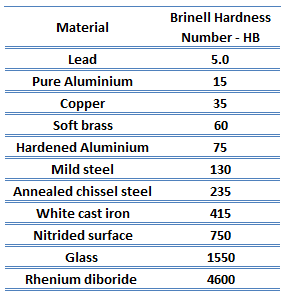
Dureza del bronce de aluminio

La dureza Brinell del bronce de aluminio – UNS C95400 es de aproximadamente 170 MPa. La dureza de los bronces de aluminio aumenta con el contenido de aluminio (y otras aleaciones), así como con las tensiones causadas por el trabajo en frío.

La prueba de dureza Rockwell  es una de las pruebas de dureza por indentación más comunes, que se ha desarrollado para las pruebas de dureza. A diferencia de la prueba de Brinell, el probador Rockwell mide la profundidad de penetración de un penetrador bajo una carga grande (carga mayor) en comparación con la penetración realizada por una precarga (carga menor). La carga menor establece la posición cero. Se aplica la carga principal y luego se retira mientras se mantiene la carga menor. La diferencia entre la profundidad de penetración antes y después de la aplicación de la carga principal se utiliza para calcular el  número de dureza Rockwell . Es decir, la profundidad de penetración y la dureza son inversamente proporcionales. La principal ventaja de la dureza Rockwell es su capacidad para  mostrar los valores de dureza directamente. El resultado es un número adimensional anotado como  HRA, HRB, HRC , etc., donde la última letra es la escala de Rockwell respectiva.

La prueba Rockwell C se realiza con un penetrador Brale ( cono de diamante de 120 ° ) y una carga mayor de 150 kg.

Ejemplo: resistencia

Suponga una varilla de plástico, que está hecha de bronce de aluminio. Esta varilla de plástico tiene un área de sección transversal de 1 cm ² . Calcule la fuerza de tracción necesaria para lograr la resistencia máxima a la tracción de este material, que es: UTS = 550 MPa.

Solución:

La tensión (σ)  se puede equiparar a la carga por unidad de área o la fuerza (F) aplicada por área de sección transversal (A) perpendicular a la fuerza como:

por lo tanto, la fuerza de tracción necesaria para lograr la máxima resistencia a la tracción es:

F = UTS x A = 550 x 10 ⁶ x 0,0001 = 55 000 N

Propiedades térmicas del bronce de aluminio

Las propiedades térmicas  de los materiales se refieren a la respuesta de los materiales a los cambios de  thermodynamics/thermodynamic-properties/what-is-temperature-physics/»>temperatura y a la aplicación de calor . A medida que un sólido absorbe thermodynamics/what-is-energy-physics/»>energía en forma de calor, su temperatura aumenta y sus dimensiones aumentan. Pero los diferentes materiales reaccionan a la aplicación de calor de manera diferente .

La capacidad calorífica , la expansión térmica y la conductividad térmica son propiedades que a menudo son críticas en el uso práctico de sólidos.

Punto de fusión del bronce de aluminio

El punto de fusión del bronce de aluminio – UNS C95400 es de alrededor de 1030 ° C.

En general, la  fusión  es un  cambio  de fase de una sustancia de la fase sólida a la líquida. El  punto  de fusión de una sustancia es la temperatura a la que se produce este cambio de fase. El  punto de fusión  también define una condición en la que el sólido y el líquido pueden existir en equilibrio.

Conductividad térmica del bronce de aluminio

La conductividad térmica del bronce de aluminio – UNS C95400 es 59 W / (mK).

Las características de transferencia de calor de un material sólido se miden mediante una propiedad llamada  conductividad térmica , k (o λ), medida en  W / mK . Es una medida de la capacidad de una sustancia para transferir calor a través de un material por  conducción . Tenga en cuenta que  la ley de Fourier se  aplica a toda la materia, independientemente de su estado (sólido, líquido o gas), por lo tanto, también se define para líquidos y gases.

La  conductividad térmica  de la mayoría de los líquidos y sólidos varía con la temperatura. Para los vapores, también depende de la presión. En general:

La mayoría de los materiales son casi homogéneos, por lo que normalmente podemos escribir  k = k (T) . Se asocian definiciones similares con las conductividades térmicas en las direcciones y y z (ky, kz), pero para un material isótropo, la conductividad térmica es independiente de la dirección de transferencia, kx = ky = kz = k.

Ejemplo: cálculo de transferencia de calor

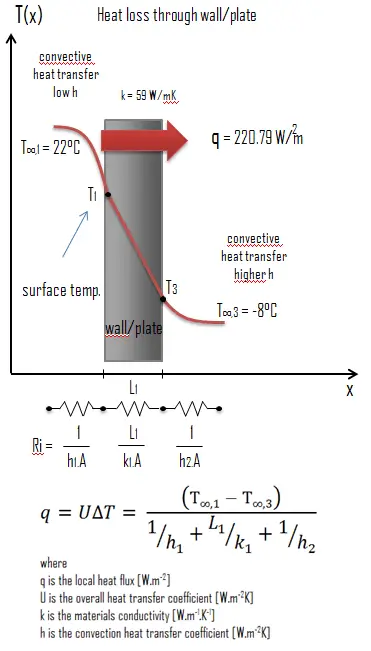La conductividad térmica se define como la cantidad de calor (en vatios) transferida a través de un área cuadrada de material de un espesor determinado (en metros) debido a una diferencia de temperatura. Cuanto menor sea la conductividad térmica del material, mayor será la capacidad del material para resistir la transferencia de calor.

Calcule la tasa de flujo de  calor a  través de una pared de 3 mx 10 m de área (A = 30 m ² ). La pared tiene 15 cm de espesor (L ₁ ) y está hecha de Bronce de Aluminio con una conductividad térmica  de k ₁ = 59 W / mK (mal aislante térmico). Suponga que las temperaturas interior y exterior  son 22 ° C y -8 ° C, y los  coeficientes de transferencia de calor por convección  en los lados interior y exterior son h ₁  = 10 W / m ² K y h ₂  = 30 W / m ² K, respectivamente. Tenga en cuenta que estos coeficientes de convección dependen en gran medida, especialmente, de las condiciones ambientales e interiores (viento, humedad, etc.).

Calcule el flujo de calor ( pérdida de calor ) a través de esta pared.

Solución:

Como se escribió, muchos de los procesos de transferencia de calor involucran sistemas compuestos e incluso involucran una combinación de  conducción  y  convección . Con estos sistemas compuestos, a menudo es conveniente trabajar con un  coeficiente de transferencia de calor en general ,  conocido como un  factor U . El factor U se define mediante una expresión análoga a  la ley de enfriamiento de Newton :

El  coeficiente de transferencia de calor general  está relacionado con la  resistencia térmica total  y depende de la geometría del problema.

Suponiendo una transferencia de calor unidimensional a través de la pared plana y sin tener en cuenta la radiación, el  coeficiente de transferencia de calor general  se puede calcular como:

El coeficiente de transferencia de calor total  es entonces: U = 1 / (1/10 + 0,15 / 59 + 1/30) = 7,36 W / m ² K

El flujo de calor se puede calcular entonces simplemente como: q = 7,36 [W / m ² K] x 30 [K] = 220,79 W / m ²

La pérdida total de calor a través de esta pared será: q _pérdida  = q. A = 220,79 [W / m ² ] x 30 [m ² ] = 6623,701 W