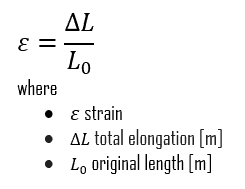En la ciencia de los materiales, la deformación también es una variable muy importante, ya que define la deformación de un objeto. A diferencia de la tensión en un objeto, que en realidad no se puede ver, la deformación es una cantidad visible y medible. Cuando tira de una barra de tensión, puede ver que la barra aumenta físicamente en longitud (o se alarga). Cuando dobla una viga, la ve curvar. Las deformaciones son un indicador directo de tensión . El comportamiento mecánico de los sólidos generalmente se define por relaciones constitutivas tensión-deformación .Cuando un metal se somete a una carga (fuerza), se distorsiona o deforma, sin importar cuán fuerte sea el metal o cuán ligera sea la carga. Si la carga es pequeña, la distorsión probablemente desaparecerá cuando se retire la carga. Tal cambio dimensional proporcional (intensidad o grado de distorsión) se llama deformación y se mide como la deformación total (alargamiento) por longitud de referencia de material debido a alguna tensión aplicada.
En mecánica de materiales, podemos definir dos tipos básicos de deformaciones:
Tensión normal
Una deformación normal resulta de la tensión de tracción y es una deformación calculada a partir de los desplazamientos relativos que se miden perpendicularmente a dos planos de referencia. Las deformaciones normales miden el movimiento perpendicular relativo de un plano de referencia con respecto a otro. El símbolo de la tensión normal suele ser el símbolo griego en minúsculas épsilon (ε).
Deformación cortante
Una deformación cortante resulta del esfuerzo cortante y es una deformación calculada a partir de los desplazamientos relativos que se miden en paralelo a dos planos de referencia. Las deformaciones cortantes miden el movimiento paralelo relativo de un plano de referencia con respecto a otro. El símbolo de la deformación por cizallamiento suele ser el símbolo griego en minúsculas gamma (γ).
& nbsp;
[/ lgc_column]
Ciencia de los materiales:
- Departamento de Energía de EE. UU., Ciencia de Materiales. DOE Fundamentals Handbook, Volumen 1 y 2. Enero de 1993.
- Departamento de Energía de EE. UU., Ciencia de Materiales. DOE Fundamentals Handbook, Volumen 2 y 2. Enero de 1993.
- William D. Callister, David G. Rethwisch. Ciencia e Ingeniería de Materiales: Introducción 9ª Edición, Wiley; 9a edición (4 de diciembre de 2013), ISBN-13: 978-1118324578.
- Eberhart, Mark (2003). Por qué se rompen las cosas: entender el mundo a través de la forma en que se desmorona. Armonía. ISBN 978-1-4000-4760-4.
- Gaskell, David R. (1995). Introducción a la Termodinámica de Materiales (4ª ed.). Taylor y Francis Publishing. ISBN 978-1-56032-992-3.
- González-Viñas, W. y Mancini, HL (2004). Introducción a la ciencia de los materiales. Prensa de la Universidad de Princeton. ISBN 978-0-691-07097-1.
- Ashby, Michael; Hugh Shercliff; David Cebon (2007). Materiales: ingeniería, ciencia, procesamiento y diseño (1ª ed.). Butterworth-Heinemann. ISBN 978-0-7506-8391-3.
- JR Lamarsh, AJ Baratta, Introducción a la ingeniería nuclear, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
[/ su_spoiler] [/ su_accordion]
[/ lgc_column]Véase más arriba:
Fuerza [/ su_button] [/ lgc_column]
Esperamos que este artículo, Deformación normal y tensión de cizallamiento , le ayude. Si es así, danos un me gusta en la barra lateral. El objetivo principal de este sitio web es ayudar al público a conocer información importante e interesante sobre los materiales y sus propiedades.
