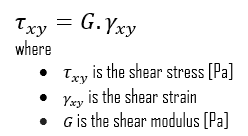La mayoría de los materiales policristalinos tienen dentro de su rango elástico una relación casi constante entre tensión y deformación. En 1678, un científico inglés llamado Robert Hooke realizó experimentos que proporcionaron datos que mostraban que en el rango elástico de un material, la deformación es proporcional a la tensión . Robert Hooke concluyó que la fuerza F en cualquier resorte es proporcional a la extensión (la deformación del estado relajado) x de la siguiente manera:
F = k · x
donde el término k es la rigidez del resorte yx es pequeño en comparación con la posible deformación total del resorte. Eventualmente debe fallar una vez que las fuerzas excedan algún límite, ya que ningún material puede comprimirse más allá de un cierto tamaño mínimo, o estirarse más allá de un tamaño máximo, sin alguna deformación permanente o cambio de estado.
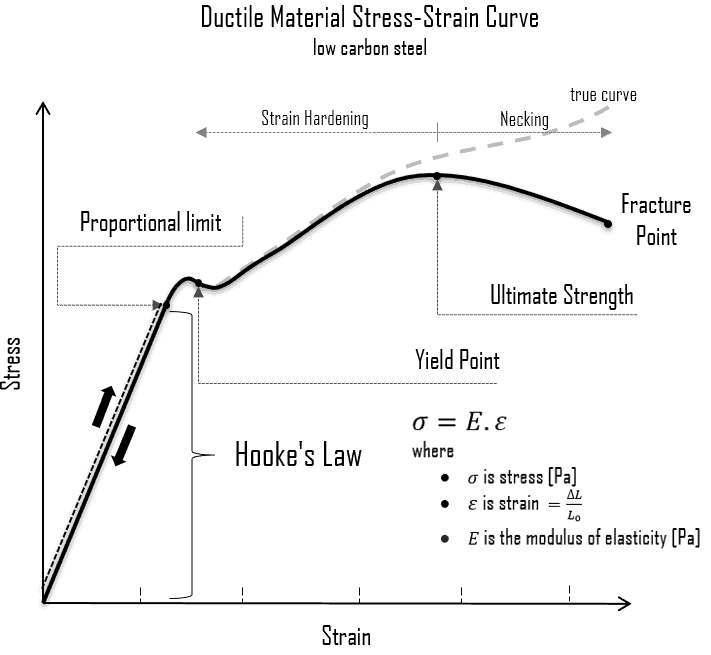
En caso de tensión de tensión de una barra uniforme (curva tensión-deformación), la ley de Hooke describe el comportamiento de una barra en la región elástica. En esta región, el alargamiento de la barra es directamente proporcional a la fuerza de tracción y la longitud de la barra e inversamente proporcional al área de la sección transversal y al módulo de elasticidad . Hasta una tensión límite, un cuerpo podrá recuperar sus dimensiones al retirar la carga. Las tensiones aplicadas hacen que los átomos de un cristal se muevan desde su posición de equilibrio. Todos los átomos se desplazan en la misma cantidad y aún mantienen su geometría relativa. Cuando se eliminan las tensiones, todos los átomos vuelven a sus posiciones originales y no se produce ninguna deformación permanente. Según la ley de Hooke,la tensión es proporcional a la deformación (en la región elástica) y la pendiente es el módulo de Young .
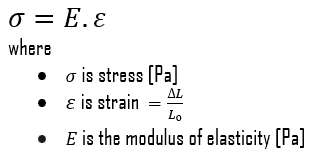Podemos extender la misma idea de relacionar el esfuerzo con la deformación y las aplicaciones de corte en la región lineal, relacionando el esfuerzo de corte con la deformación de corte para crear la ley de Hooke para el esfuerzo de corte :
Para materiales isotrópicos dentro de la región elástica, puede relacionar la relación de Poisson (ν), el módulo de elasticidad de Young (E) y el módulo de elasticidad de corte (G):
Los módulos elásticos relevantes para los materiales policristalinos:
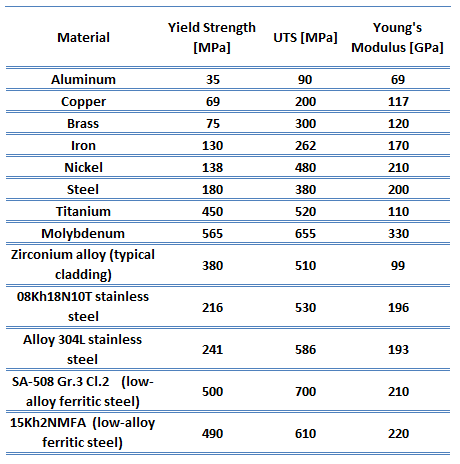Módulo de elasticidad de Young. El módulo de elasticidad de Young es el módulo de elasticidad para esfuerzos de tracción y compresión en el régimen de elasticidad lineal de una deformación uniaxial y generalmente se evalúa mediante ensayos de tracción.- Módulo de elasticidad a cortante. El módulo de corte, o módulo de rigidez, se deriva de la torsión de una probeta cilíndrica. Describe la respuesta del material al esfuerzo cortante. Su símbolo es G. El módulo de corte es una de varias cantidades para medir la rigidez de los materiales y surge en la ley de Hooke generalizada.
- Módulo de elasticidad a granel. El módulo de elasticidad volumétrico describe la elasticidad volumétrica o la tendencia de un objeto a deformarse en todas las direcciones cuando se carga uniformemente en todas las direcciones. Por ejemplo, describe la respuesta elástica a la presión hidrostática y la tensión equilátera (como la presión en el fondo del océano o una piscina profunda). También es propiedad de un material la que determina la respuesta elástica a la aplicación de tensión. Para un fluido, solo el módulo volumétrico es significativo.
[/ lgc_column]
Ciencia de los materiales:
- Departamento de Energía de EE. UU., Ciencia de Materiales. DOE Fundamentals Handbook, Volumen 1 y 2. Enero de 1993.
- Departamento de Energía de EE. UU., Ciencia de Materiales. DOE Fundamentals Handbook, Volumen 2 y 2. Enero de 1993.
- William D. Callister, David G. Rethwisch. Ciencia e Ingeniería de Materiales: Introducción 9ª Edición, Wiley; 9a edición (4 de diciembre de 2013), ISBN-13: 978-1118324578.
- Eberhart, Mark (2003). Por qué se rompen las cosas: entender el mundo a través de la forma en que se desmorona. Armonía. ISBN 978-1-4000-4760-4.
- Gaskell, David R. (1995). Introducción a la Termodinámica de Materiales (4ª ed.). Taylor y Francis Publishing. ISBN 978-1-56032-992-3.
- González-Viñas, W. y Mancini, HL (2004). Introducción a la ciencia de los materiales. Prensa de la Universidad de Princeton. ISBN 978-0-691-07097-1.
- Ashby, Michael; Hugh Shercliff; David Cebon (2007). Materiales: ingeniería, ciencia, procesamiento y diseño (1ª ed.). Butterworth-Heinemann. ISBN 978-0-7506-8391-3.
- JR Lamarsh, AJ Baratta, Introducción a la ingeniería nuclear, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
[/ su_spoiler] [/ su_accordion]
[/ lgc_column]Véase más arriba:
Fuerza [/ su_button] [/ lgc_column]
Esperamos que este artículo, la ley de Hooke , le ayude. Si es así, danos un me gusta en la barra lateral. El objetivo principal de este sitio web es ayudar al público a conocer información importante e interesante sobre los materiales y sus propiedades.
