Qu’est-ce que le module d’élasticité – Module d’élasticité – Définition

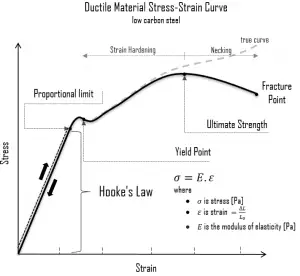
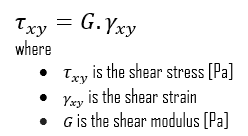En cas de contrainte de traction d’une barre uniforme (courbe contrainte-déformation), la loi de Hooke décrit le comportement d’une barre dans la région élastique. Dans cette région, l’allongement de la barre est directement proportionnel à la force de traction et à la longueur de la barre et inversement proportionnel à la section transversale et au module d’élasticité. Jusqu’à une contrainte limite, une caisse pourra retrouver ses dimensions au retrait de la charge. Les contraintes appliquées font que les atomes d’un cristal se déplacent de leur position d’équilibre. Tous les atomes sont déplacés de la même quantité et conservent toujours leur géométrie relative. Lorsque les contraintes sont supprimées, tous les atomes reviennent à leur position d’origine et aucune déformation permanente ne se produit. Selon la loi de Hooke, la contrainte est proportionnelle à la déformation (dans la région élastique) et la pente est le module de Young.

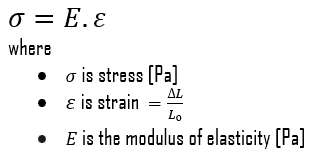Nous pouvons étendre la même idée de relier la contrainte à la déformation aux applications de cisaillement dans la région linéaire, en reliant la contrainte de cisaillement à la déformation de cisaillement pour créer la loi de Hooke pour la contrainte de cisaillement:

Pour les matériaux isotropes dans la région élastique, vous pouvez relier le coefficient de Poisson (ν), le module de Young (E) et le module d’élasticité de cisaillement (G):

Les modules élastiques propres aux matériaux polycristallins :

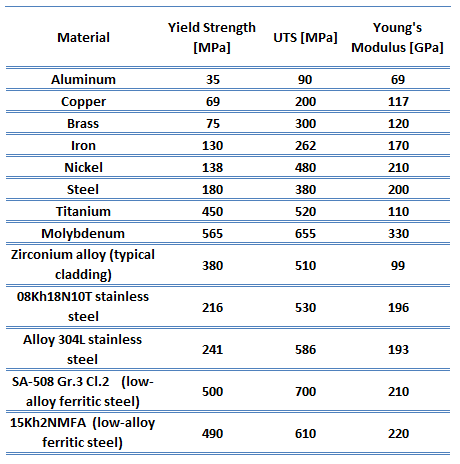• Module  de Young. Le module  de Young est le module d’élasticité pour les contraintes de traction et de compression dans le régime d’élasticité linéaire d’une déformation uniaxiale et est généralement évalué par des essais de traction.
• Module d’élasticité de cisaillement. Le module de cisaillement, ou module de rigidité, est dérivé de la torsion d’une éprouvette cylindrique. Il décrit la réponse du matériau à la contrainte de cisaillement. Son symbole est G. Le module de cisaillement est l’une des nombreuses quantités permettant de mesurer la rigidité des matériaux et il apparaît dans la loi de Hooke généralisée.
• Module d’élasticité de masse. Le module d’élasticité de masse décrit l’élasticité volumétrique ou la tendance d’un objet à se déformer dans toutes les directions lorsqu’il est uniformément chargé dans toutes les directions. Par exemple, il décrit la réponse élastique à la pression hydrostatique et à la tension équilatérale (comme la pression au fond de l’océan ou d’une piscine profonde). C’est aussi la propriété d’un matériau qui détermine la réponse élastique à l’application d’une contrainte. Pour un fluide, seul le module de masse est significatif.

1. Département américain de l’énergie, science des matériaux. DOE Fundamentals Handbook, Volume 1 et 2. Janvier 1993.
2. Département américain de l’énergie, science des matériaux. DOE Fundamentals Handbook, Volume 2 et 2. Janvier 1993.
3. William D. Callister, David G. Rethwisch. Science et génie des matériaux : une introduction 9e édition, Wiley ; 9 édition (4 décembre 2013), ISBN-13 : 978-1118324578.
4. En ligneEberhart, Mark (2003). Pourquoi les choses se cassent : Comprendre le monde par la manière dont il se décompose. Harmonie. ISBN 978-1-4000-4760-4.
5. Gaskell, David R. (1995). Introduction à la thermodynamique des matériaux (4e éd.). Éditions Taylor et Francis. ISBN 978-1-56032-992-3.
6. Gonzalez-Viñas, W. & Mancini, HL (2004). Une introduction à la science des matériaux. Presse universitaire de Princeton. ISBN 978-0-691-07097-1
7. Ashby, Michael; Hugh Shercliff; David Cebon (2007). Matériaux: ingénierie, science, traitement et conception (1ère éd.). Butterworth-Heinemann. ISBN 978-0-7506-8391-3.
8. JR Lamarsh, AJ Baratta, Introduction au génie nucléaire, 3e éd., Prentice-Hall, 2001, ISBN : 0-201-82498-1.

Voir au dessus:

Loi de Hooke