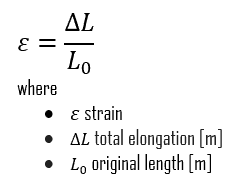What is Normal strain and Shear Strain - Definition

In mechanics of materials, we can define two basic types of strain: A normal strain results from tensile stress. A shear strain results from shear stress.

In materials science, strain is also very important variable, since it defines the deformation of an object. Unlike stress in an object, which you can’t actually see, deformation is a visible and measurable quantity. When you pull on a tension rod, you can see the rod physically increase in length (or elongate). When you bend a beam, you see it curve. Deformations are a direct indicator of strain. The mechanical behavior of solids is usually defined by constitutive stress-strain relations. When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. If the load is small, the distortion will probably disappear when the load is removed. Such a proportional dimensional change (intensity or degree of the distortion) is called strain and is measured as the total deformation (elongation) per reference length of material due to some applied stress.

In mechanics of materials, we can define two basic types of strain:

Normal strain

A normal strain results from tensile stress and is a strain computed from relative displacements that are measured perpendicular to two reference planes. Normal strains measure the relative perpendicular movement of one reference plane with respect to another. The symbol for normal strain is usually the lowercase Greek symbol epsilon (ε).

Shear strain

A shear strain results from shear stress and it is a strain computed from relative displacements that are measured parallel to two reference planes. Shear strains measure the relative parallel movement of one reference plane with respect to another. The symbol for shear strain is usually the lowercase Greek symbol gamma (γ ).

References:

Materials Science:

U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 2 and 2. January 1993.
William D. Callister, David G. Rethwisch. Materials Science and Engineering: An Introduction 9th Edition, Wiley; 9 edition (December 4, 2013), ISBN-13: 978-1118324578.
Eberhart, Mark (2003). Why Things Break: Understanding the World by the Way It Comes Apart. Harmony. ISBN 978-1-4000-4760-4.
Gaskell, David R. (1995). Introduction to the thermodynamics of Materials (4th ed.). Taylor and Francis Publishing. ISBN 978-1-56032-992-3.
González-Viñas, W. & Mancini, H.L. (2004). An Introduction to Materials Science. Princeton University Press. ISBN 978-0-691-07097-1.
Ashby, Michael; Hugh Shercliff; David Cebon (2007). Materials: engineering, science, processing and design (1st ed.). Butterworth-Heinemann. ISBN 978-0-7506-8391-3.
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.

See above:

Strength

We hope, this article, Normal strain and Shear Strain, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.