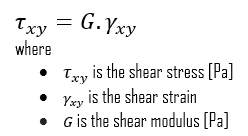We can extend the same idea of relating stress to strain to shear applications in the linear region, relating shear stress to shear strain to create Hooke’s law for shear stress:
For isotropic materials within the elastic region, you can relate Poisson’s ratio (ν), Young’s modulus of elasticity (E), and the shear modulus of elasticity (G):
Shear Modulus of Elasticity
The shear modulus, or the modulus of rigidity, is derived from the torsion of a cylindrical test piece. It describes the material’s response to shear stress. Its symbol is G. The shear modulus is one of several quantities for measuring the stiffness of materials and it arises in the generalized Hooke’s law.
 Shear stress. Shear stress exists when two parts of a material tend to slide across each other in any typical plane of shear upon application of force parallel to that plane. Torsion is a variation of pure shear in which a structural member is twisted. Torsional forces produce a rotational motion about the longitudinal axis of one end of the member relative to the other end. Shear stress is also of great importance in nature, being intimately related to the downslope movement of earth materials (as in case of avalanches).
Shear stress. Shear stress exists when two parts of a material tend to slide across each other in any typical plane of shear upon application of force parallel to that plane. Torsion is a variation of pure shear in which a structural member is twisted. Torsional forces produce a rotational motion about the longitudinal axis of one end of the member relative to the other end. Shear stress is also of great importance in nature, being intimately related to the downslope movement of earth materials (as in case of avalanches).- Shear strains. A shear strain results from shear stress and it is a strain computed from relative displacements that are measured parallel to two reference planes. Shear strains measure the relative parallel movement of one reference plane with respect to another. The symbol for shear strain is usually the lowercase Greek symbol gamma (γ ).
We hope, this article, Shear Modulus of Elasticity, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.