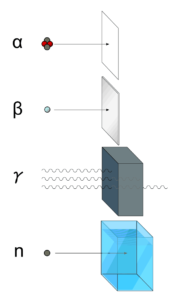
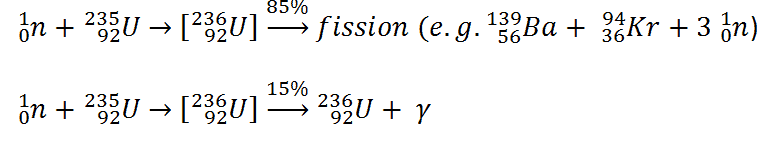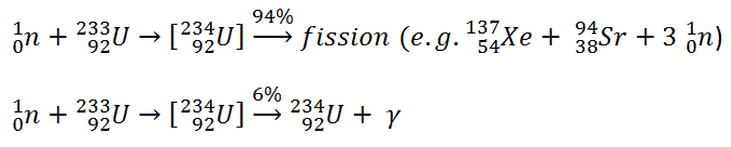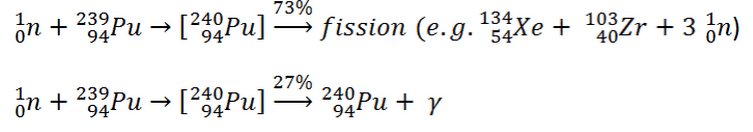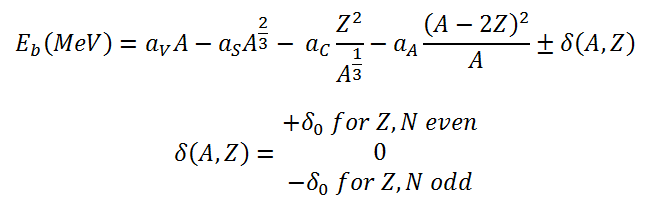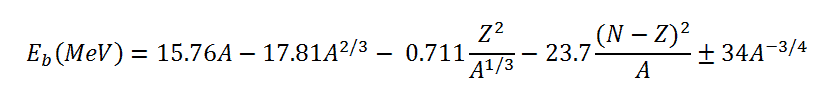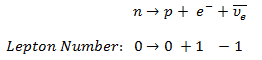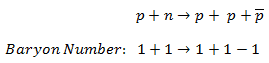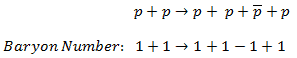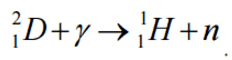- Significance of the source
- Intensity. The rate of neutrons emitted by the source.
- Energy distribution of emitted neutrons.
- Angular distribution of emitted neutrons.
- Mode of emission. Continuous or pulsed operation.
Classification by significance of the source
- Large (Significant) neutron sources
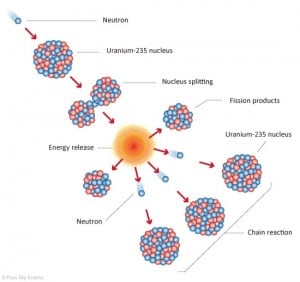
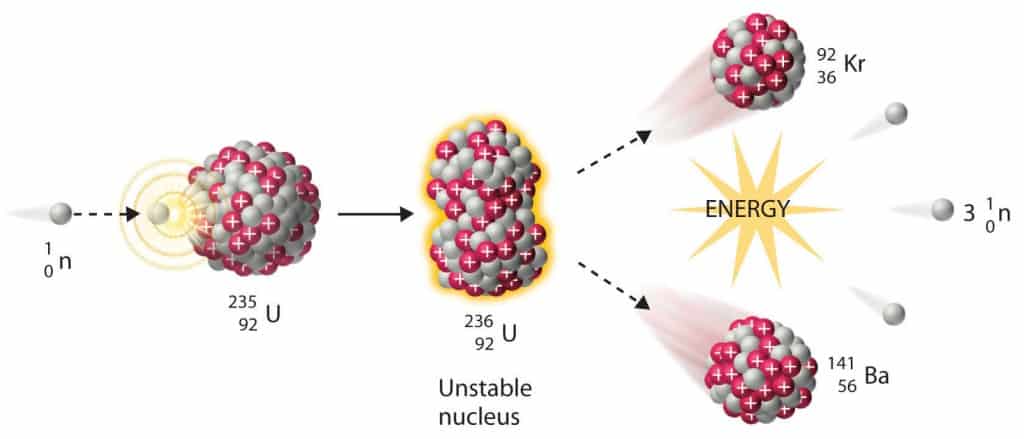
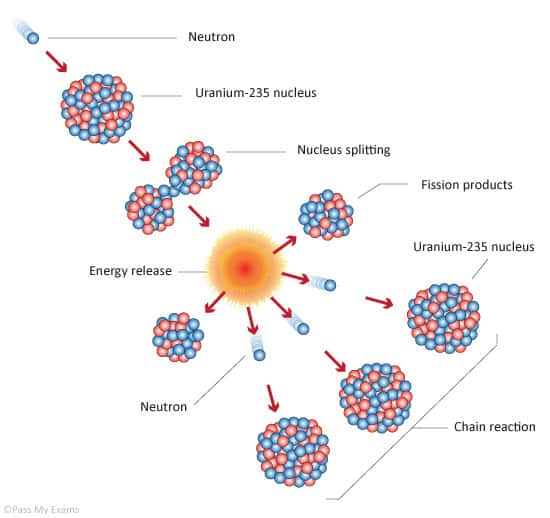
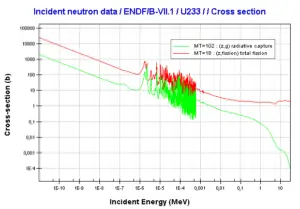
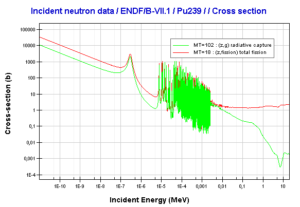
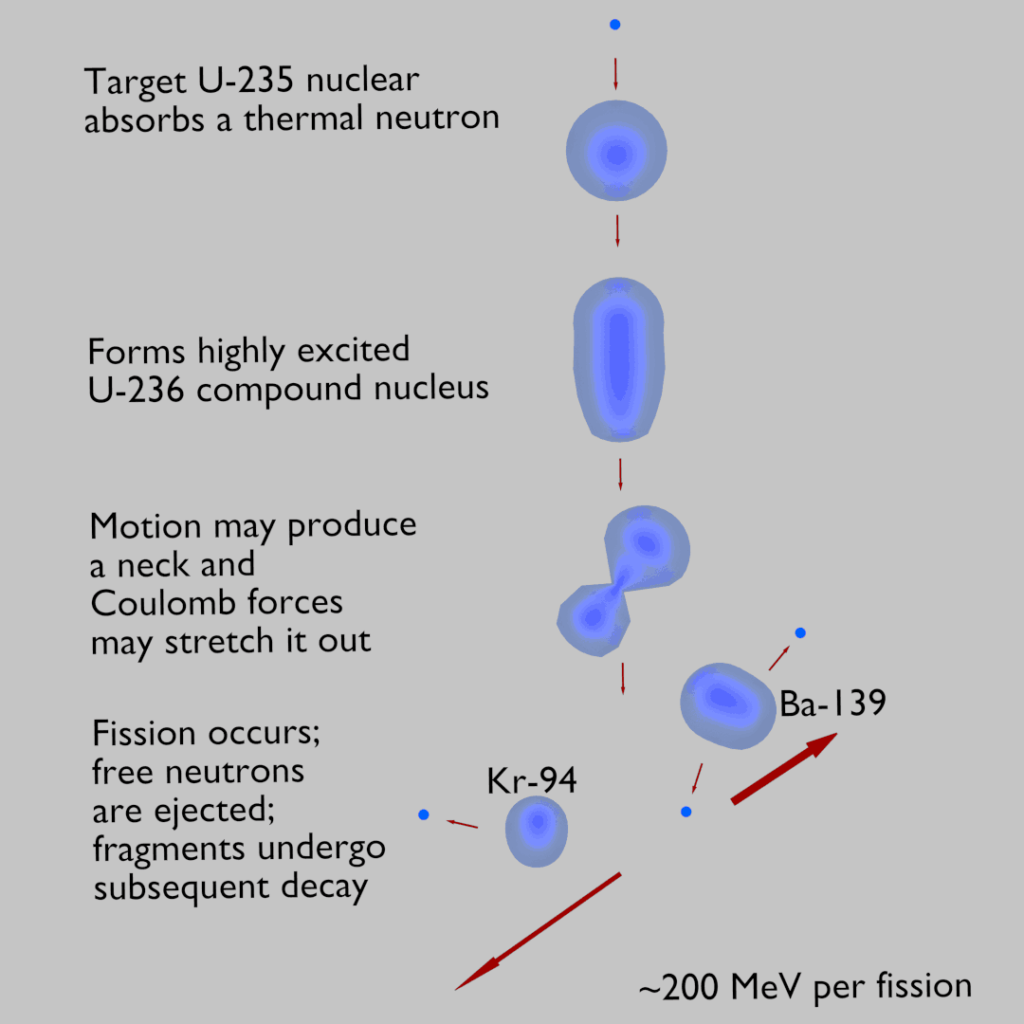
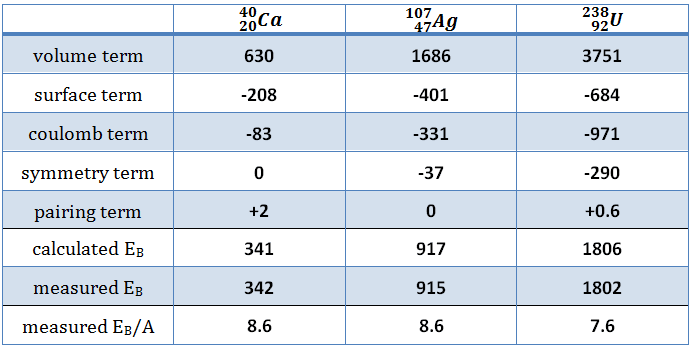
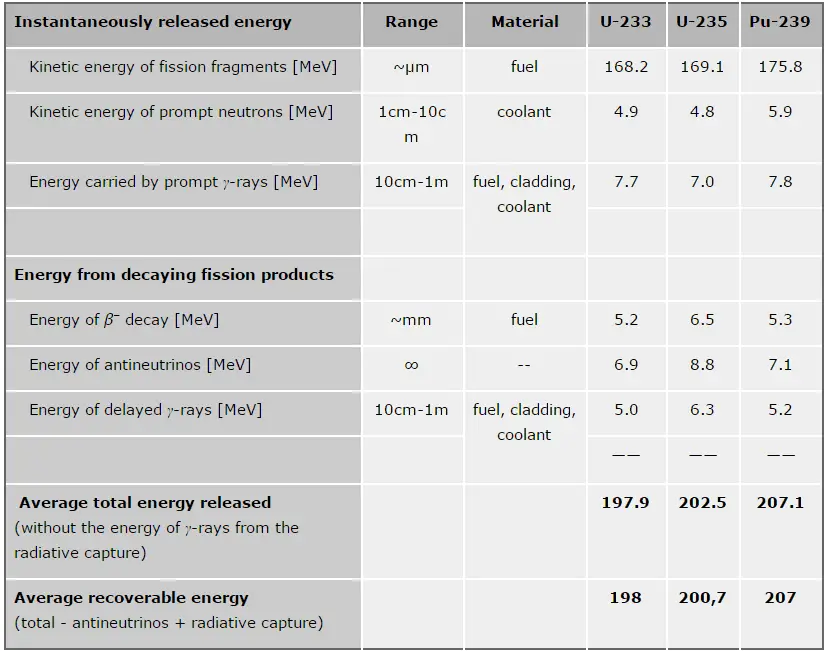
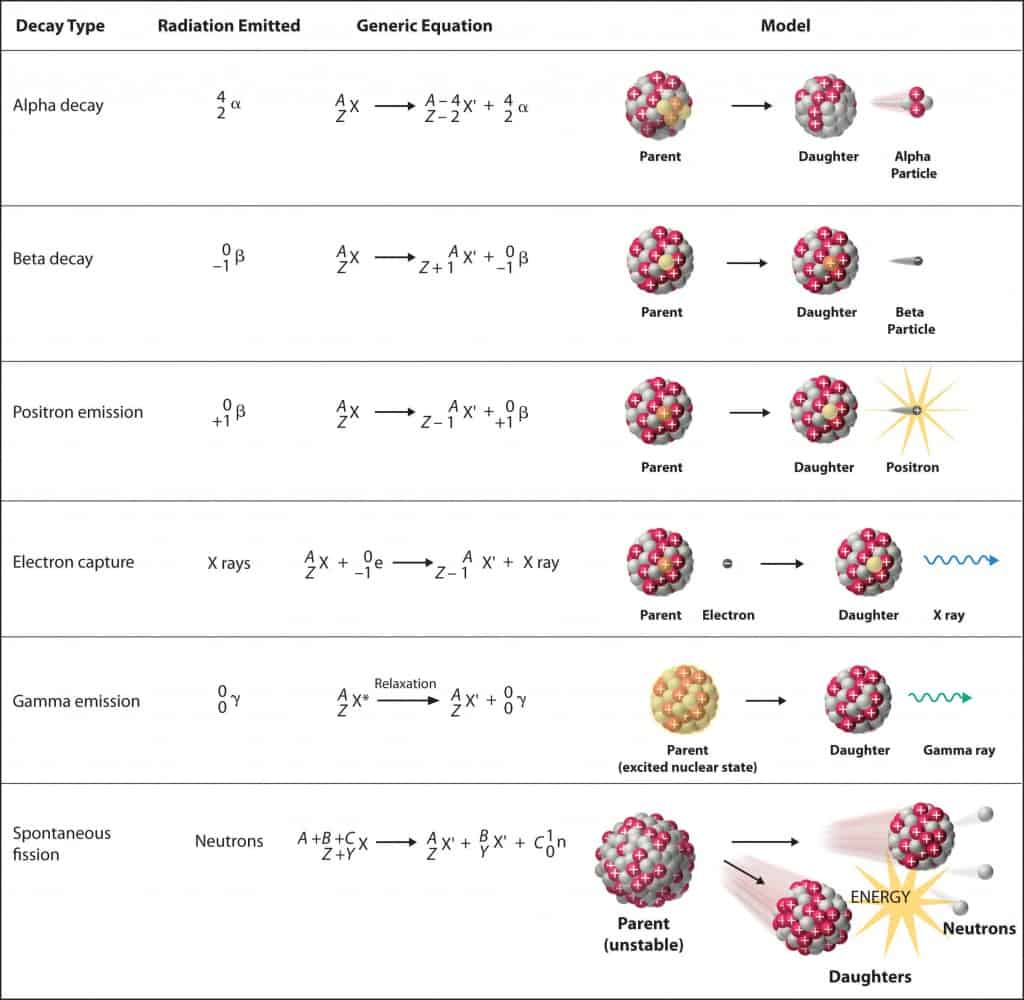
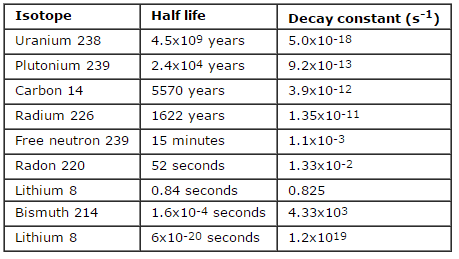
- Nuclear Reactors. There are nuclei that can undergo fission on their own spontaneously, but only certain nuclei, like uranium-235, uranium-233 and plutonium-239, can sustain a fission chain reaction. This is because these nuclei release neutrons when they break apart, and these neutrons can induce fission of other nuclei. Uranium-235 which exists as 0.7% of naturally occurring uranium undergoes nuclear fission with thermal neutrons with the production of, on average, 2.4 fast neutrons and the release of ~ 180 MeV of energy per fission. Free neutrons released by each fission play very important role as a trigger of the reaction, but they can be also used fo another purpose. For example: One neutron is required to trigger a further fission. Part of free neutrons (let say 0.5 neutrons/fission) is absorbed in other material, but an excess of neutrons (0.9 neutrons/fission) is able to leave the surface of the reactor core and can be used as a neutron source.
-
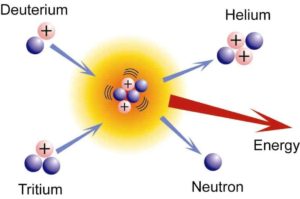
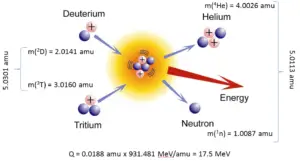
- Fusion Systems. Nuclear fusion is a nuclear reaction in which two or more atomic nuclei (e.g. D+T) collide at a very high energy and fuse together. Thy byproduct of DT fusion is a free neutron (see picture), therefore also nuclear fusion reaction has the potential to produces large quantities of neutrons.
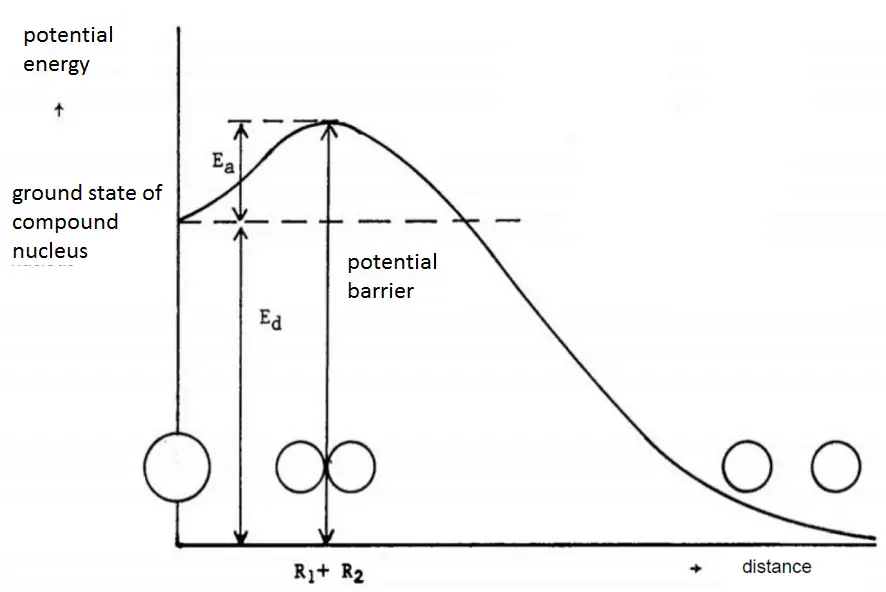
- Spallation Sources. A spallation source is a high-flux neutron source in which protons that have been accelerated to high energies hit a heavy target material, causing the emission of neutrons. The reaction occurs above a certain energy threshold for the incident particle, which is typically 5 – 15 MeV.
- Medium neutron sources
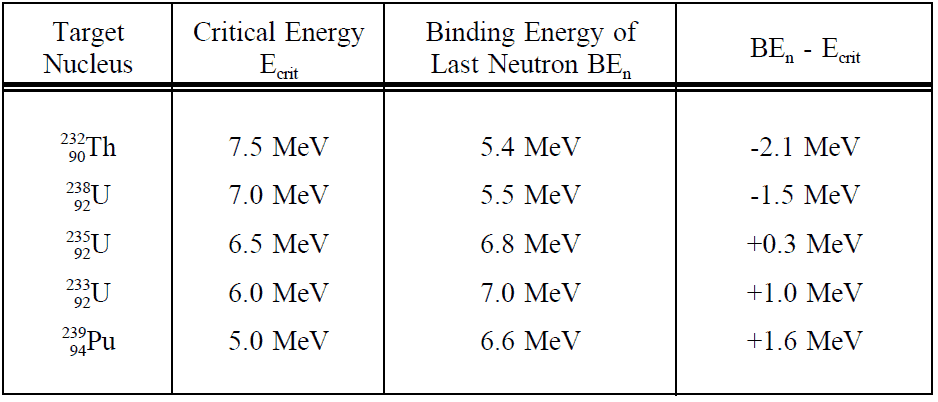
- Bremssstrahlung from Electron Accelerators / Photofission. Energetic electrons when slowed down rapidly in a heavy target emit intense gamma radiation during the deceleration process. This is known as Bremsstrahlung or braking radiation. The interaction of the gamma radiation with the target produces neutrons via the (γ,n) reaction, or the (γ,fission) reaction when a fissile target is used. e-→Pb → γ→ Pb →(γ,n) and (γ,fission). The Bremsstrahlung γ energy exceeds the binding energy of the “last” neutron in the target. A source strength of 1013 neutrons/second produced in short (i.e. < 5 μs) pulses can be readily realised.
- Dense plasme focus. The dense plasma focus (DPF) is a device that is known as an efficient source of neutrons from fusion reactions. Mechanism of dense plasma focus (DPF) is based on nuclear fusion of short-lived plasma of deuterium and/or tritium. This device produces a short-lived plasma by electromagnetic compression and acceleration that is called a pinch. This plasma is during the pinch hot and dense enough to cause nuclear fusion and the emission of neutrons.
- Light ion accelerators. Neutrons can be also produced by particle accelerators using targets of deuterium, tritium, lithium, beryllium, and other low-Z materials. In this case the target must be bombarded with accelerated hydrogen (H), deuterium (D), or tritium (T) nuclei.
- Small neutron sources
- Neutron Generators. Neutrons are produced in the fusion of deuterium and tritium in the following exothermic reaction. 2D + 3T → 4He + n + 17.6 MeV. The neutron is produced with a kinetic energy of 14.1 MeV. This can be achieved on a small scale in the laboratory with a modest 100 kV accelerator for deuterium atoms bombarding a tritium target. Continuous neutron sources of ~1011 neutrons/second can be achieved relatively simply.
- Radioisotope source – (α,n) reactions. In certain light isotopes the ‘last’ neutron in the nucleus is weakly bound and is released when the compound nucleus formed following α-particle bombardment decays. The bombardment of beryllium by α-particles leads to the production of neutrons by the following exothermic reaction: 4He + 9Be→12C + n + 5.7 MeV. This reaction yields a weak source of neutrons with an energy spectrum resembling that from a fission source and is used nowadays in portable neutron sources. Radium, plutonium or americium can be used as an α-emitter.
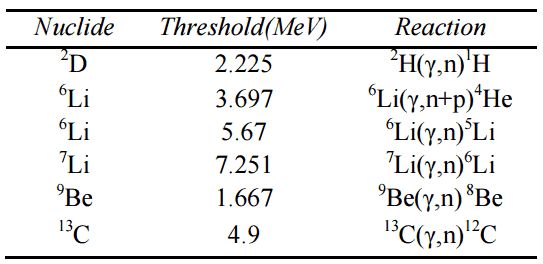
- Radioisotope source – (γ,n) reactions. (γ,n) reactions can also be used for the same purpose. In this type of source, because of the greater range of the γ-ray, the two physical components of the source can be separated making it possible to ‘switch off’ the reaction if so required by removing the radioactive source from the beryllium. (γ,n) sources produce a monoenergetic neutrons unlike (α,n) sources. The (γ,n) source uses antimony-124 as the gamma emitter in the following endothermic reaction.
124Sb→124Te + β− + γ
γ + 9Be→8Be + n – 1.66 MeV
-
- Radioisotope source – spontaneous fission. Certain isotopes undergo spontaneous fission with emission of neutrons. The most commonly used spontaneous fission source is the radioactive isotope californium-252. Cf-252 and all other spontaneous fission neutron sources are produced by irradiating uranium or another transuranic element in a nuclear reactor, where neutrons are absorbed in the starting material and its subsequent reaction products, transmuting the starting material into the SF isotope.
| Neutron Source | Example | Neutron Yield | Released Energy
MeV / neutron |
| (α,n) reactions | Radium-Beryllium source | 8 x 10-5 / α | 6,600,000 |
| (D,T) fusion | 400 keV deuterons in neutron generator | 4 x 10-5 / deuteron | 10,000 |
| Electron Bremsstrahlung
/ Photofission |
100 MeV electrons on uranium | 5 x 10-2 / electron | 2,000 |
| Fission | Induced fission of U-235 in thermal reactor | 1 / fission | 180 |
| Spallation | 800 MeV protons on uranium | 30 / proton | 55 |
| (D,T) fusion | Inertial confinement fusion | 1 / fusion | 18 |
We hope, this article, Neutron Source, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.