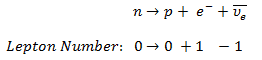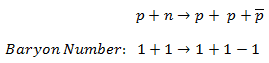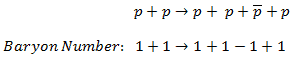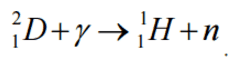A nuclear reaction is considered to be the process in which two nuclear particles (two nuclei or a nucleus and a nucleon) interact to produce two or more nuclear particles or ˠ-rays (gamma rays). Thus, a nuclear reaction must cause a transformation of at least one nuclide to another. Sometimes if a nucleus interacts with another nucleus or particle without changing the nature of any nuclide, the process is referred to a nuclear scattering, rather than a nuclear reaction. Perhaps the most notable nuclear reactions are the nuclear fusion reactions of light elements that power the energy production of stars and the Sun. Natural nuclear reactions occur also in the interaction between cosmic rays and matter.
The most notable man-controlled nuclear reaction is the fission reaction which occurs in nuclear reactors. Nuclear reactors are devices to initiate and control a nuclear chain reaction, but there are not only manmade devices. The world’s first nuclear reactor operated about two billion years ago. The natural nuclear reactor formed at Oklo in Gabon, Africa, when a uranium-rich mineral deposit became flooded with groundwater that acted as a neutron moderator, and a nuclear chain reaction started. These fission reactions were sustained for hundreds of thousands of years, until a chain reaction could no longer be supported. This was confirmed by existence of isotopes of the fission-product gas xenon and by different ratio of U-235/U-238 (enrichment of natural uranium).
See also: TALYS – a software for the simulation of nuclear reactions.
See also: JANIS – Java-based Nuclear Data Information System
Notation of Nuclear Reactions
Standard nuclear notation shows (see picture) the chemical symbol, the mass number and the atomic number of the isotope.
If the initial nuclei are denoted by a and b, and the product nuclei are denoted by c and d, the reaction can be represented by the equation:
a + b → c + d
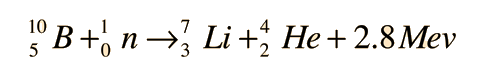
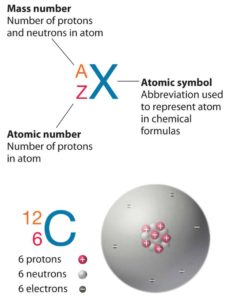
Source: chemwiki.ucdavis.edu
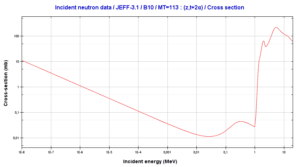
Instead of using the full equations in the style above, in many situations a compact notation is used to describe nuclear reactions. This style of the form a(b,c)d is equivalent to a + b producing c + d. Light particles are often abbreviated in this shorthand, typically p means proton, n means neutron, d means deuteron, α means an alpha particle or helium-4, β means beta particle or electron, γ means gamma photon, etc. The reaction above would be written as 10B(n,α)7Li.
Basic Classification of Nuclear Reactions
In order to understand the nature of neutron nuclear reactions, the classification according to the time scale of of these reactions has to be introduced. Interaction time is critical for defining the reaction mechanism.
There are two extreme scenarios for nuclear reactions (not only neutron reactions):
- A projectile and a target nucleus are within the range of nuclear forces for the very short time allowing for an interaction of a single nucleon only. These type of reactions are called the direct reactions.
- A projectile and a target nucleus are within the range of nuclear forces for the time allowing for a large number of interactions between nucleons. These type of reactions are called the compound nucleus reactions.
In fact, there is always some non-direct (multiple internuclear interaction) component in all reactions, but the direct reactions have this component limited.
Types of Nuclear Reactions
Although the number of possible nuclear reactions is enormous, nuclear reactions can be sorted by types. Most of nuclear reactions are accompanied by gamma emission. Some examples are:
- Elastic scattering. Occurs, when no energy is transferred between the target nucleus and the incident particle.
208Pb (n, n) 208Pb
- Inelastic scattering. Occurs, when energy is transferred. The difference of kinetic energies is saved in excited nuclide.
40Ca (α, α’) 40mCa
- Capture reactions. Both charged and neutral particles can be captured by nuclei. This is accompanied by the emission of ˠ-rays. Neutron capture reaction produces radioactive nuclides (induced radioactivity).
238U (n, ˠ) 239U
- Transfer Reactions. The absorption of a particle accompanied by the emission of one or more particles is called the transfer reaction.
4He (α, p) 7Li
- Fission reactions. Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei). The fission process often produces free neutrons and photons (in the form of gamma rays), and releases a large amount of energy.
235U (n, 3 n) fission products
- Fusion reactions. Occur when, two or more atomic nuclei collide at a very high speed and join to form a new type of atomic nucleus.The fusion reaction of deuterium and tritium is particularly interesting because of its potential of providing energy for the future.
3T (d, n) 4He
- Spallation reactions. Occur, when a nucleus is hit by a particle with sufficient energy and momentum to knock out several small fragments or, smash it into many fragments.
- Nuclear decay (Radioactive decay). Occurs when an unstable atom loses energy by emitting ionizing radiation. Radioactive decay is a random process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay. There are many types of radioactive decay:
- Alpha radioactivity. Alha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus. Because of its very large mass (more than 7000 times the mass of the beta particle) and its charge, it heavy ionizes material and has a very short range.
-
- Beta radioactivity. Beta particles are high-energy, high-speed electrons or positrons emitted by certain types of radioactive nuclei such as potassium-40. The beta particles have greater range of penetration than alpha particles, but still much less than gamma rays.The beta particles emitted are a form of ionizing radiation also known as beta rays. The production of beta particles is termed beta decay.
-
- Gamma radioactivity. Gamma rays are electromagnetic radiation of an very high frequency and are therefore high energy photons. They are produced by the decay of nuclei as they transition from a high energy state to a lower state known as gamma decay. Most of nuclear reactions are accompanied by gamma emission.
-
- Neutron emission. Neutron emission is a type of radioactive decay of nuclei containing excess neutrons (especially fission products), in which a neutron is simply ejected from the nucleus. This type of radiation plays key role in nuclear reactor control, because these neutrons are delayed neutrons.
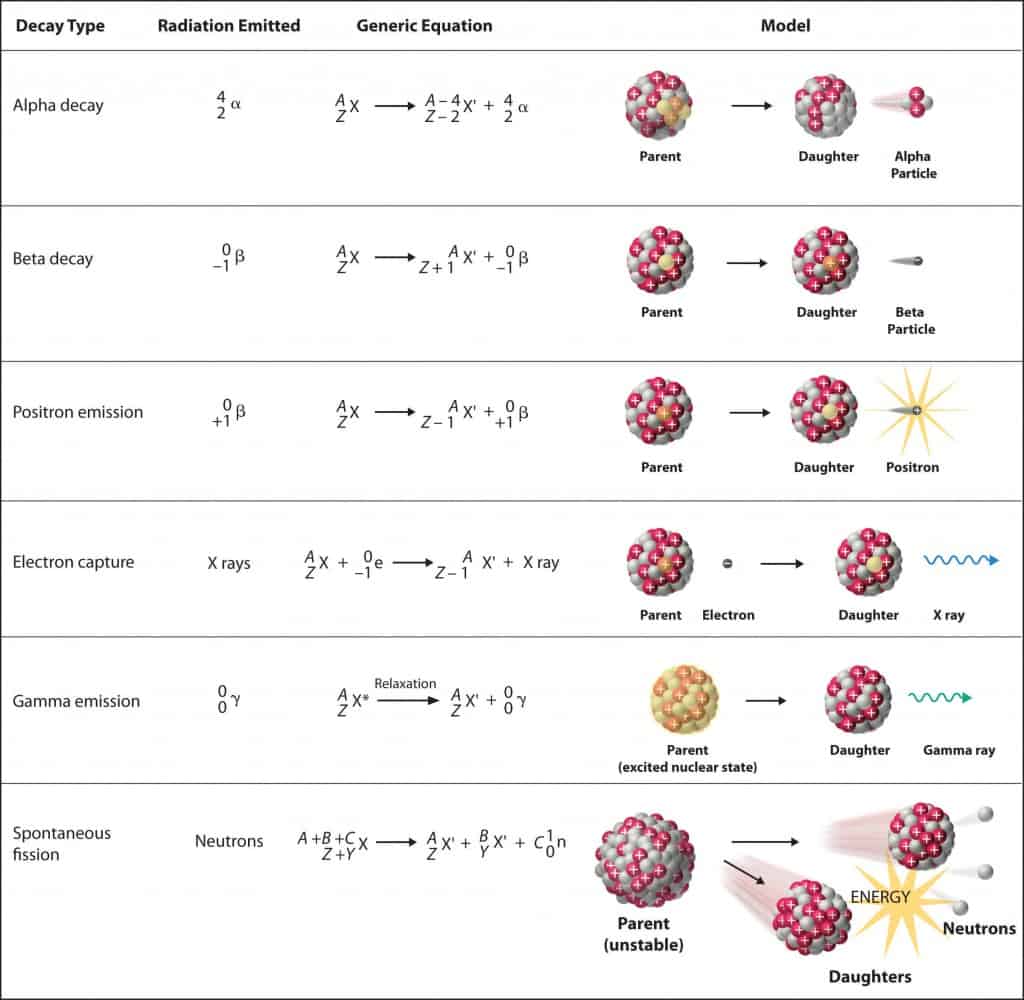
Source: chemwiki.ucdavis.edu
Conservation Laws in Nuclear Reactions
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for charge, momentum, angular momentum, and energy(including rest energies). Additional conservation laws, not anticipated by classical physics, are:
Some conservation principles have arisen from theoretical considerations, others are just empirical relationships. Notwithstanding, any reaction not expressly forbidden by the conservation laws will generally occur, if perhaps at a slow rate. This expectation is based on quantum mechanics. Unless the barrier between the initial and final states is infinitely high, there is always a non-zero probability that a system will make the transition between them.
For purposes of analyzing non-relativistic reactions, it is sufficient to note four of the fundamental laws governing these reactions.
- Conservation of nucleons. The total number of nucleons before and after a reaction are the same.
- Conservation of charge. The sum of the charges on all the particles before and after a reaction are the same
- Conservation of momentum. The total momentum of the interacting particles before and after a reaction are the same.
- Conservation of energy. Energy, including rest mass energy, is conserved in nuclear reactions.
Reference: Lamarsh, John R. Introduction to Nuclear engineering 2nd Edition.
Energetics of Nuclear Reactions – Q-value
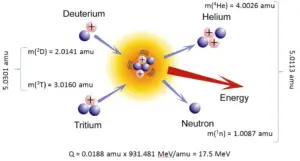
In nuclear and particle physics the energetics of nuclear reactions is determined by the Q-value of that reaction. The Q-value of the reaction is defined as the difference between the sum of the masses of the initial reactants and the sum of the masses of the final products, in energy units (usually in MeV).
Consider a typical reaction, in which the projectile a and the target A gives place to two products, B and b. This can also be expressed in the notation that we used so far, a + A → B + b, or even in a more compact notation, A(a,b)B.
See also: E=mc2
The Q-value of this reaction is given by:
Q = [ma + mA – (mb + mB)]c2
which is the same as the excess kinetic energy of the final products:
Q = Tfinal – Tinitial
= Tb + TB – (Ta + TA)
For reactions in which there is an increase in the kinetic energy of the products Q is positive. The positive Q reactions are said to be exothermic (or exergic). There is a net release of energy, since the kinetic energy of the final state is greater than the kinetic energy of the initial state.
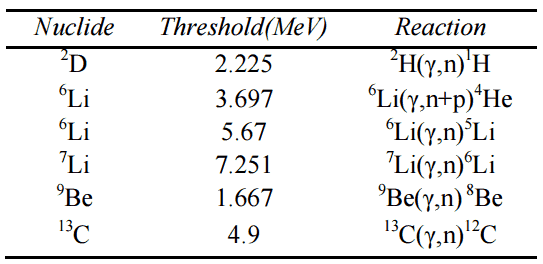
For reactions in which there is a decrease in the kinetic energy of the products Q is negative. The negative Q reactions are said to be endothermic (or endoergic) and they require a net energy input.
The energy released in a nuclear reaction can appear mainly in one of three ways:
- Kinetic energy of the products
- Emission of gamma rays. Gamma rays are emitted by unstable nuclei in their transition from a high energy state to a lower state known as gamma decay.
- Metastable state. Some energy may remain in the nucleus, as a metastable energy level.
A small amount of energy may also emerge in the form of X-rays. Generally, products of nuclear reactions may have different atomic numbers, and thus the configuration of their electron shells is different in comparison with reactants. As the electrons rearrange themselves and drop to lower energy levels, internal transition X-rays (X-rays with precisely defined emission lines) may be emitted.
See also: Q-value Calculator
Exothermic Reactions
Endothermic Reactions
Test your Knowledge – Nuclear Reactions
With our simple quizzes, you can test your knowledge.
It is intuitive: start quiz and answer questions.
We hope, this article, Nuclear Reaction, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.