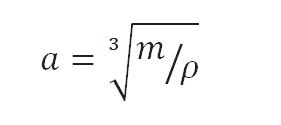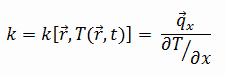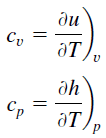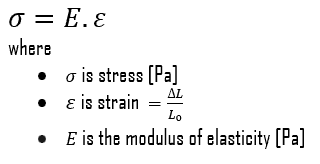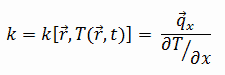About Austenitic Stainless Steel – Type 304
Type 304 stainless steel (containing 18%-20% chromium and 8%-10.5% nickel) is the most common stainless steel. It is also known as “18/8” stainless steel because of its composition, which includes 18% chromium and 8% nickel. This alloy resists most types of corrosion. It is an austenitic stainless steel and it has also excellent cryogenic properties, and good high-temperature strength as well as good forming and welding properties. It is less electrically and thermally conductive than carbon steel and is essentially non-magnetic.
Type 304L stainless steel, which is widely used in nuclear industry, is an extra-low carbon version of the 304 steel alloy. This grade has slightly lower mechanical properties than the standard 304 grade, but is still widely used thanks to its versatility. The lower carbon content in 304L minimizes deleterious or harmful carbide precipitation as a result of welding. 304L can, therefore, be used “as welded” in severe corrosion environments, and it eliminates the need for annealing. Grade 304 has also good oxidation resistance in intermittent service to 870 °C, and in continuous service to 925 °C.
The body of the reactor vessel is constructed of a high-quality low-alloy carbon steel, and all surfaces that come into contact with reactor coolant are clad with a minimum of about 3 to 10 mm of austenitic stainless steel in order to minimize corrosion. Since grade 304L does not require post-weld annealing, it is extensively used in heavy gauge components.
Summary
| Name | Austenitic Stainless Steel |
| Phase at STP | solid |
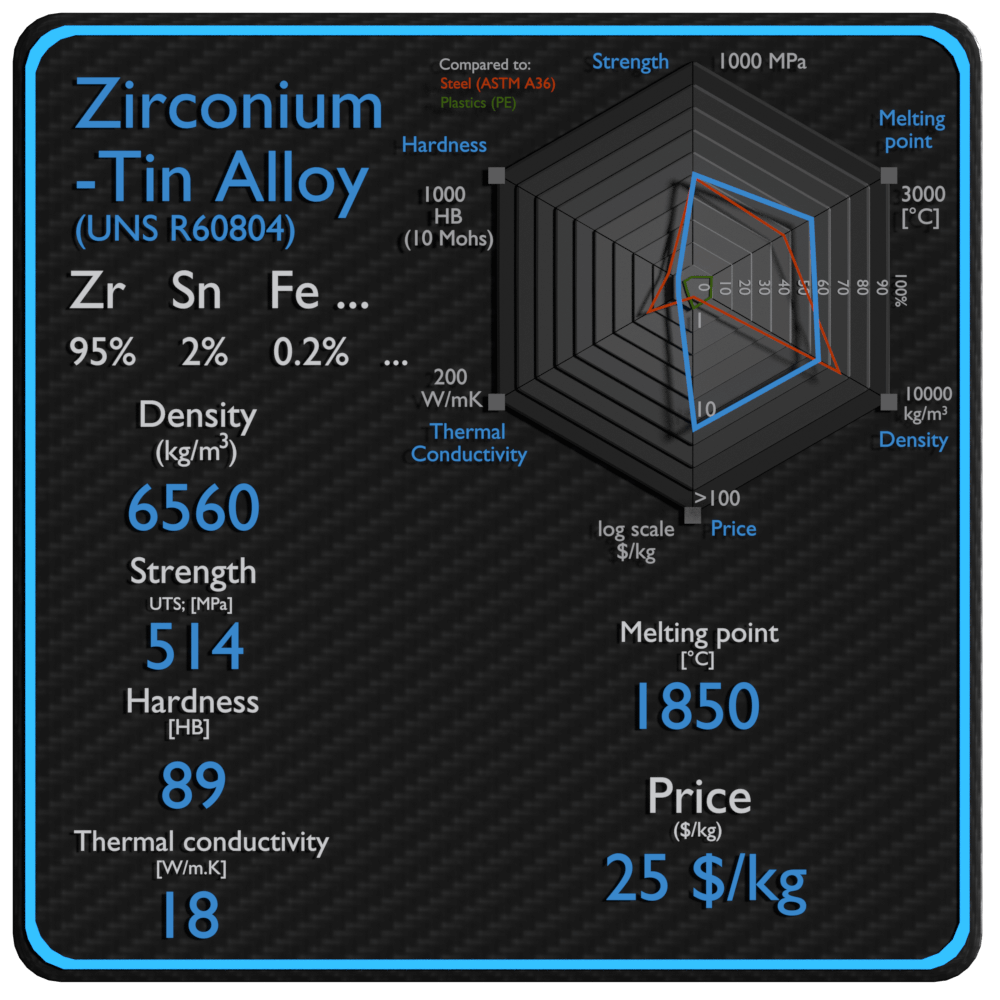
| Density | 7850 kg/m3 |
| Ultimate Tensile Strength | 515 MPa |
| Yield Strength | 205 MPa |
| Young’s Modulus of Elasticity | 193 GPa |
| Brinell Hardness | 201 BHN |
| Melting Point | 1450 °C |
| Thermal Conductivity | 20 W/mK |
| Heat Capacity | 500 J/g K |
| Price | 2 $/kg |
Density of Austenitic Stainless Steel
Typical densities of various substances are at atmospheric pressure. Density is defined as the mass per unit volume. It is an intensive property, which is mathematically defined as mass divided by volume: ρ = m/V
In words, the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance. The standard SI unit is kilograms per cubic meter (kg/m3). The Standard English unit is pounds mass per cubic foot (lbm/ft3).
Density of Austenitic Stainless Steel is 7850 kg/m3.
Example: Density
Calculate the height of a cube made of Austenitic Stainless Steel, which weighs one metric ton.
Solution:
Density is defined as the mass per unit volume. It is mathematically defined as mass divided by volume: ρ = m/V
As the volume of a cube is the third power of its sides (V = a3), the height of this cube can be calculated:
The height of this cube is then a = 0.503 m.
Density of Materials
Mechanical Properties of Austenitic Stainless Steel
Strength of Austenitic Stainless Steel
In mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. Strength of materials basically considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. In designing structures and machines, it is important to consider these factors, in order that the material selected will have adequate strength to resist applied loads or forces and retain its original shape.
Strength of a material is its ability to withstand this applied load without failure or plastic deformation. For tensile stress, the capacity of a material or structure to withstand loads tending to elongate is known as ultimate tensile strength (UTS). Yield strength or yield stress is the material property defined as the stress at which a material begins to deform plastically whereas yield point is the point where nonlinear (elastic + plastic) deformation begins. In case of tensional stress of a uniform bar (stress-strain curve), the Hooke’s law describes behaviour of a bar in the elastic region. The Young’s modulus of elasticity is the elastic modulus for tensile and compressive stress in the linear elasticity regime of a uniaxial deformation and is usually assessed by tensile tests.
See also: Strength of Materials
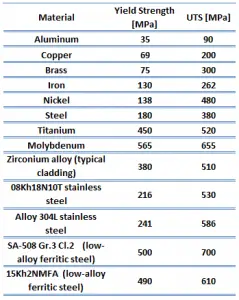
Ultimate Tensile Strength of Austenitic Stainless Steel
Ultimate tensile strength of Austenitic Stainless Steel is 280 MPa.
Yield Strength of Austenitic Stainless Steel
Yield strength of Austenitic Stainless Steel is 145 MPa.
Modulus of Elasticity of Austenitic Stainless Steel
The Young’s modulus of elasticity of Austenitic Stainless Steel is 45 GPa.
Hardness of Austenitic Stainless Steel
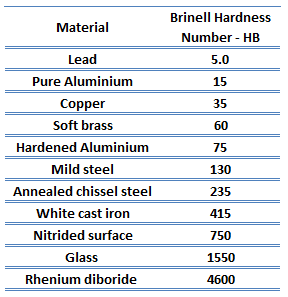
In materials science, hardness is the ability to withstand surface indentation (localized plastic deformation) and scratching. Brinell hardness test is one of indentation hardness tests, that has been developed for hardness testing. In Brinell tests, a hard, spherical indenter is forced under a specific load into the surface of the metal to be tested.
The Brinell hardness number (HB) is the load divided by the surface area of the indentation. The diameter of the impression is measured with a microscope with a superimposed scale. The Brinell hardness number is computed from the equation:
Brinell hardness of Austenitic Stainless Steel is approximately 70 BHN(converted).
See also: Hardness of Materials
Example: Strength
Assume a plastic rod, which is made of Austenitic Stainless Steel. This plastic rod has a cross-sectional area of 1 cm2. Calculate the tensile force needed to achieve the ultimate tensile strength for this material, which is: UTS = 280 MPa.
Solution:
Stress (σ) can be equated to the load per unit area or the force (F) applied per cross-sectional area (A) perpendicular to the force as:
therefore, the tensile force needed to achieve the ultimate tensile strength is:
F = UTS x A = 280 x 106 x 0.0001 = 28 000 N
Thermal Properties of Austenitic Stainless Steel
Austenitic Stainless Steel – Melting Point
Melting point of Austenitic Stainless Steel is 550-640 °C.
Note that, these points are associated with the standard atmospheric pressure. In general, melting is a phase change of a substance from the solid to the liquid phase. The melting point of a substance is the temperature at which this phase change occurs. The melting point also defines a condition in which the solid and liquid can exist in equilibrium. For various chemical compounds and alloys, it is difficult to define the melting point, since they are usually a mixture of various chemical elements.
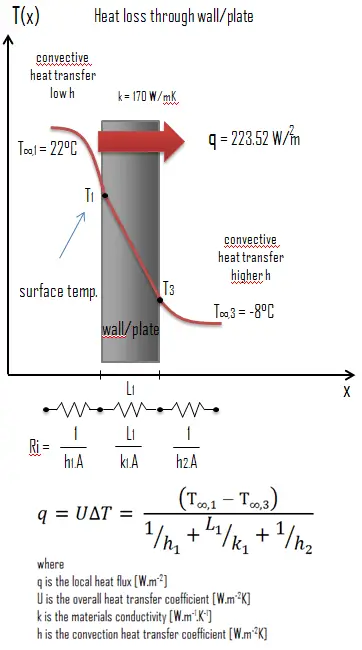
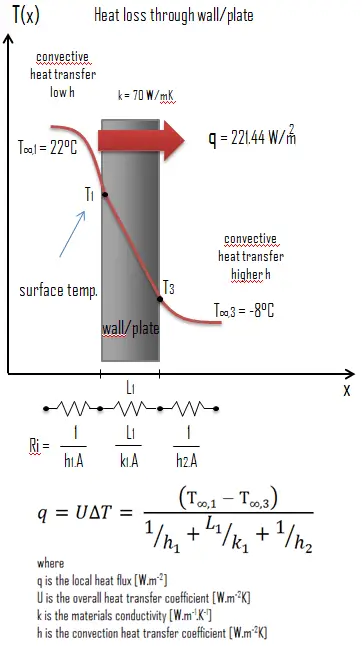
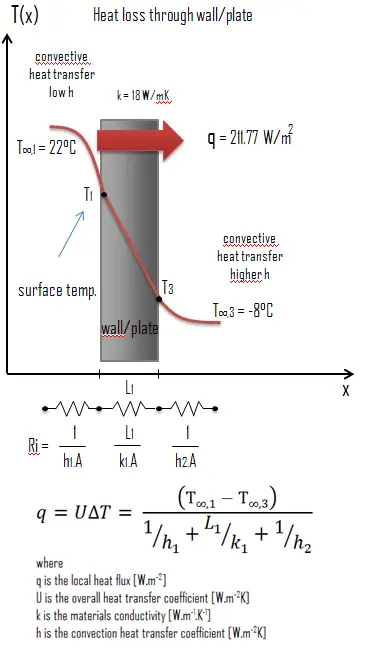
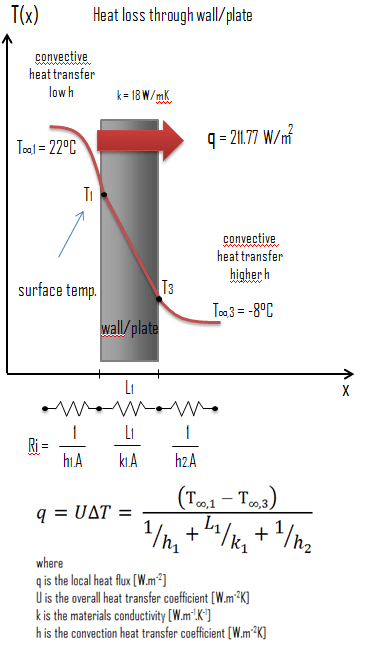
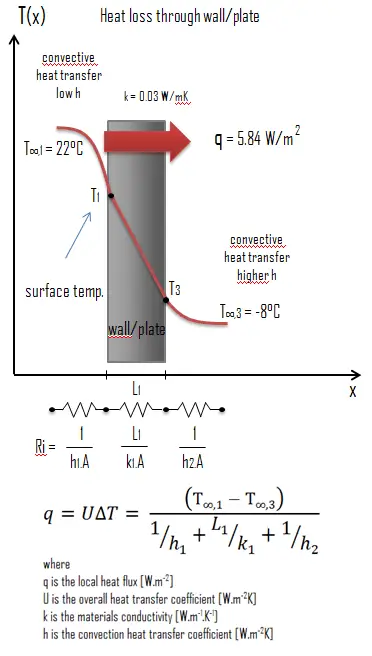
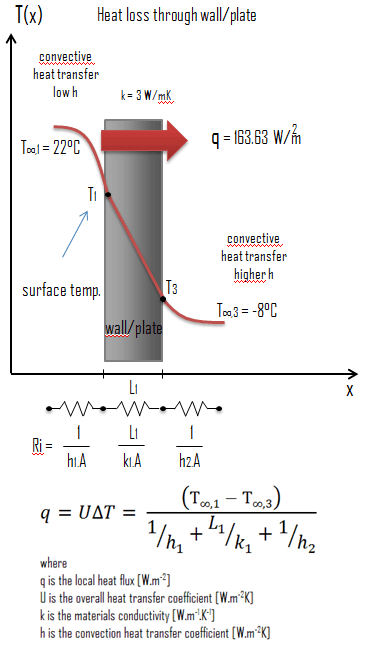
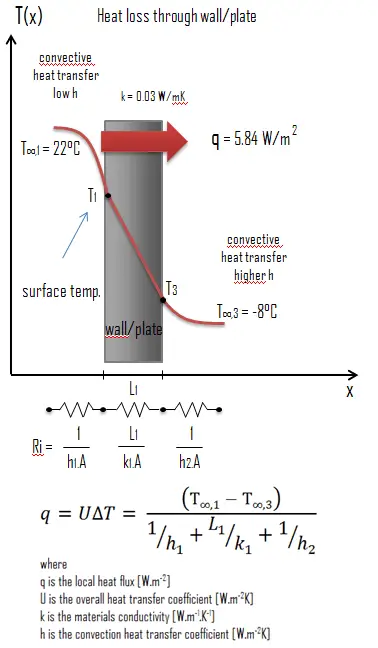
Austenitic Stainless Steel – Thermal Conductivity
Thermal conductivity of Austenitic Stainless Steel is 116 W/(m·K).
The heat transfer characteristics of a solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It is a measure of a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies for all matter, regardless of its state (solid, liquid, or gas), therefore, it is also defined for liquids and gases.
The thermal conductivity of most liquids and solids varies with temperature. For vapors, it also depends upon pressure. In general:
Most materials are very nearly homogeneous, therefore we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.
Austenitic Stainless Steel – Specific Heat
Specific heat of Austenitic Stainless Steel is 900 J/g K.
Specific heat, or specific heat capacity, is a property related to internal energy that is very important in thermodynamics. The intensive properties cv and cp are defined for pure, simple compressible substances as partial derivatives of the internal energy u(T, v) and enthalpy h(T, p), respectively:
where the subscripts v and p denote the variables held fixed during differentiation. The properties cv and cp are referred to as specific heats (or heat capacities) because under certain special conditions they relate the temperature change of a system to the amount of energy added by heat transfer. Their SI units are J/kg K or J/mol K.