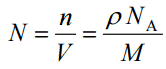Atomic Number
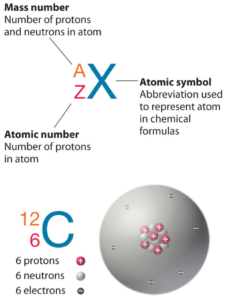
The atom consist of a small but massive nucleus surrounded by a cloud of rapidly moving electrons. The nucleus is composed of protons and neutrons. The total number of protons in the nucleus of an atom is called the atomic number (or the proton number) of the atom and is given the symbol Z.
The number of electrons in an electrically-neutral atom is the same as the number of protons in the nucleus. The total electrical charge of the nucleus is therefore +Ze, where e (elementary charge) equals to 1,602 x 10-19coulombs. Each electron is influenced by the electric fields produced by the positive nuclear charge and the other (Z – 1) negative electrons in the atom.
Since the number of electrons is responsible for the chemical bavavior of atoms, the atomic number identifies the various chemical elements.
The chemical properties of the atom are determined by the number of protons, in fact, by number and arrangement of electrons. The configuration of these electrons follows from the principles of quantum mechanics. The number of electrons in each element’s electron shells, particularly the outermost valence shell, is the primary factor in determining its chemical bonding behavior. In the periodic table, the elements are listed in order of increasing atomic number Z.
Hydrogen (H), for example , consist of one electron and one proton. The number of neutrons in a nucleus is known as the neutron number and is given the symbol N. The total number of nucleons, that is, protons and neutrons in a nucleus, is equal to Z + N = A, where A is called the mass number. The various species of atoms whose nuclei contain particular numbers of protons and neutrons are called nuclides. Each nuclide is denoted by chemical symbol of the element (this specifies Z) with tha atomic mass number as supescript.
Thus the symbol 1H refers to the nuclide of hydrogen with a single proton as nucleus. 2H is the hydrogen nuclide with a neutron as well as a proton in the nucleus (2H is also called deuterium or heavy hydrogen). Atoms such as 1H, 2H whose nuclei contain the same number of protons but different number of neutrons (different A) are known as isotopes.
Atomic Number and Nuclear Stability
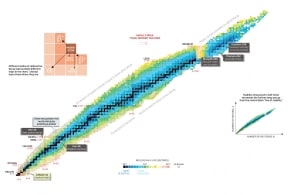
Nuclear Stability is a concept that helps to identify the stability of an isotope. To identify the stability of an isotope it is needed to find the ratio of neutrons to protons. To determine the stability of an isotope you can use the ratio neutron/proton (N/Z). Also to help understand this concept there is a chart of the nuclides, known as a Segre chart. This chart shows a plot of the known nuclides as a function of their atomic and neutron numbers. It can be observed from the chart that there are more neutrons than protons in nuclides with Z greater than about 20 (Calcium). These extra neutrons are necessary for stability of the heavier nuclei. The excess neutrons act somewhat like nuclear glue.
See also: Livechart – iaea.org
Atomic nuclei consist of protons and neutrons, which attract each other through the nuclear force, while protons repel each other via the electric force due to their positive charge. These two forces compete, leading to various stability of nuclei. There are only certain combinations of neutrons and protons, which forms stable nuclei.
Neutrons stabilize the nucleus, because they attract each other and protons , which helps offset the electrical repulsion between protons. As a result, as the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many or too few neutrons for a given number of protons, the resulting nucleus is not stable and it undergoes radioactive decay. Unstable isotopesdecay through various radioactive decay pathways, most commonly alpha decay, beta decay, or electron capture. Many other rare types of decay, such as spontaneous fission or neutron emission are known. It should be noted that all of these decay pathways may be accompanied by the subsequent emission of gamma radiation. Pure alpha or beta decays are very rare.
Atomic Number – Does it conserve in a nuclear reaction?
In general, the atomic number is not conserved in nuclear reactions.
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for charge, momentum, angular momentum, and energy (including rest energies). Additional conservation laws, not anticipated by classical physics, are are electric charge, lepton number and baryon number. Certain of these laws are obeyed under all circumstances, others are not. We have accepted conservation of energy and momentum. In reactor physics (non-relativistic physics), we assume that the number of protons (the atomic number), the number of neutrons (the neutron number) and its sum (the atomic mass number) are usually separately conserved. We shall find circumstances and conditions in which this rule is not true. Where we are considering non-relativistic nuclear reactions, it is essentially true. However, where we are considering relativistic nuclear energies or those involving the weak interactions (e.g. in beta decay the atomic number is not conserved), we shall find that these principles must be extended.
Conservation of Electric Charge
As was written, the total electrical charge of the nucleus is determined by the atomic number and is equal to +Ze. Conservation of charge is thought to be a universal conservation law. No experimental evidence for any violation of this principle has ever been observed.
For example:
Consider a typical fission reaction such as the one listed below.
Typically, when uranium 235 nucleus undergoes fission, the nucleus splits into two smaller nuclei (triple fission can also rarely occur), along with a few neutrons (the average is 2.43 neutrons per fission by thermal neutron) and release of energy in the form of heat and gamma rays. From these reactions we find that in the fission the parent nucleus:
- 235U contains 92 protons (a charge of +92e),
- incident neutron is electrically neutral.
The fission fragments:
- 139Ba contains 56 protons (a charge of +56e),
- 94Ba contains 36 protons (a charge of +36e)
We see that the total charge is 92e before and after the reaction; thus, charge is conserved. It is noteworthy, the total number of nucleons before and after a reaction are also the same.
High Atomic Number Materials Use – Shielding of Gamma Radiation
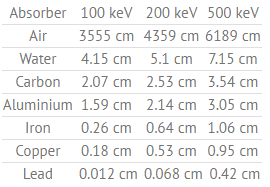
In short, effective shielding of gamma radiation is in most cases based on use of materials with two following material properties:
- high-density of material.
- high atomic number of material (high Z materials)
However, low-density materials and low Z materials can be compensated with increased thickness, which is as significant as density and atomic number in shielding applications.
A lead is widely used as a gamma shield. Major advantage of lead shield is in its compactness due to its higher density. On the other hand depleted uranium is much more effective due to its higher Z. Depleted uranium is used for shielding in portable gamma ray sources.
In nuclear power plants shielding of a reactor core can be provided by materials of reactor pressure vessel, reactor internals (neutron reflector). Also heavy concrete is usually used to shield both neutrons and gamma radiation.
Although water is neither high density nor high Z material, it is commonly used as gamma shields. Water provides a radiation shielding of fuel assemblies in a spent fuel pool during storage or during transports from and into the reactor core.
Atomic Number Density
Atomic number should not be confused with the atomic number density, which completely different physical quantity.
In nuclear physics, the macroscopic cross-section represents the effective target area of all of the nuclei contained in the volume of the material. The macroscopic cross-section is derived from microscopic cross-sectionand the atomic number density (N):
Σ=σ.N
In this equation, the atomic number density plays the crucial role as the microscopic cross-section, because in the reactor core the atomic number density of certain materials (e.g. water as the moderator) can be simply changed leading into certain reactivity changes. In order to understand the nature of these reactivity changes, we must understand the term the atomic number density.
The atomic number density (N; atoms/cm3) is the number of atoms of a given type per unit volume (V; cm3) of the material. The atomic number density (N; atoms/cm3) of a pure material having atomic or molecular weight (M; grams/mol) and the material density (⍴; gram/cm3) is easily computed from the following equation using Avogadro’s number (NA = 6.022×1023 atoms or molecules per mole):
We hope, this article, Atomic Number, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.