Facebook Instagram Youtube Twitter

What is E=mc2 Meaning – Definition

E=mc2 is the equivalence of the mass and energy. Each nuclear process can be evaluated from an E = mc2 perspective. E=mc2 meaning. Material Properties

E = mc2 Meaning

At the beginning of the 20th century, the notion of mass underwent a radical revision. Mass lost its absoluteness. One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible one into the other. Equivalence of the mass and energy is described by Einstein’s famous formula E = mc2. In words, energy equals mass multiplied by the speed of light squared. Because the speed of light is a very large number, the formula implies that any small amount of matter contains a very large amount of energy. The mass of an object was seen to be equivalent to energy, to be interconvertible with energy, and to increase significantly at exceedingly high speeds near that of light. The total energy of an object was understood to comprise its rest mass as well as its increase of mass caused by increase in kinetic energy.

In special theory of relativity certain types of matter may be created or destroyed, but in all of these processes, the mass and energy associated with such matter remains unchanged in quantity. It was found the rest mass an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E = mc2) this binding energy is proportional to this mass difference and it is known as the mass defect.

E=mc2 represents the new conservation principle – the conservation of mass-energy.

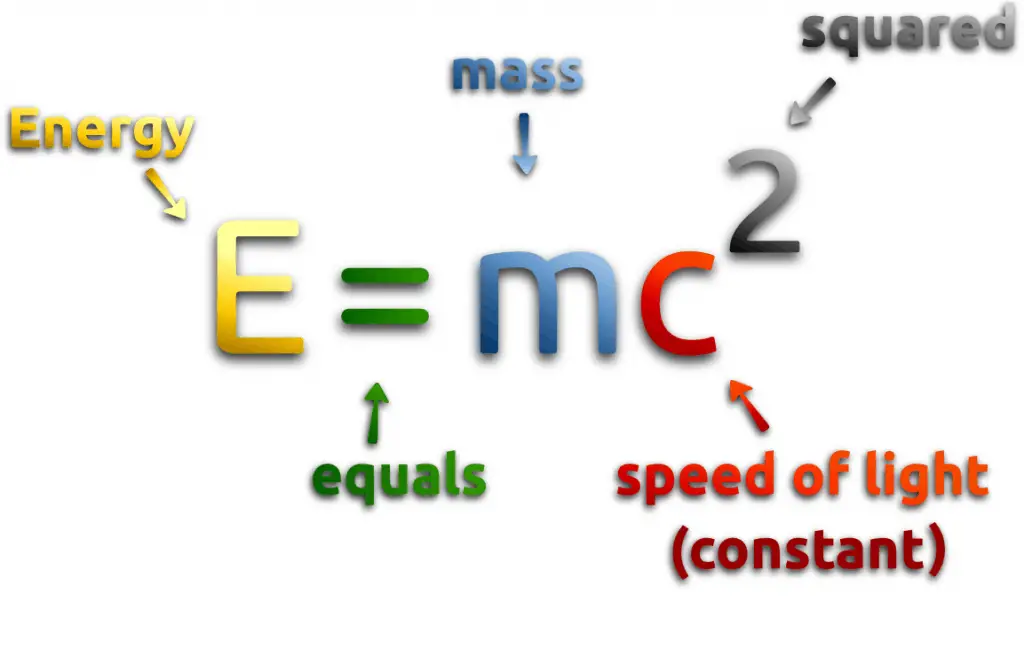
E=MC2 - Nuclear energy
This formule describes equivalence of mass and energy.

, where m is the small amount of mass and c is the speed of light.

What that means? If the nuclear energy is generated (splitting atoms, nuclear fusion), a small amount of mass (saved in the nuclear binding energy) transforms into the pure energy (such as kinetic energy, thermal energy, or radiant energy).

Example:

The energy equivalent of one gram (1/1000 of a kilogram) of mass is equivalent to:

  • 89.9 terajoules
  • 25.0 million kilowatt-hours (≈ 25 GW·h)
  • 21.5 billion kilocalories (≈ 21 Tcal)
  • 85.2 billion BTUs

or to the energy released by combustion of the following:

  • 21.5 kilotons of TNT-equivalent energy (≈ 21 kt)
  • 568,000 US gallons of automotive gasoline

Any time energy is generated, the process can be evaluated from an E = mc2 perspective.

 
Example: Mass defect of a 63Cu
Calculate the mass defect of a 63Cu nucleus if the actual mass of 63Cu in its nuclear ground state is 62.91367 u.

63Cu nucleus has 29 protons and also has (63 – 29) 34 neutrons.

The mass of a proton is 1.00728 u and a neutron is 1.00867 u.

The combined mass is: 29 protons x (1.00728 u/proton) + 34 neutrons x (1.00867 u/neutron) = 63.50590 u

The mass defect is Δm = 63.50590 u – 62.91367 u =  0.59223 u

Convert the mass defect into energy (nuclear binding energy).

(0.59223 u/nucleus) x (1.6606 x 10-27 kg/u) = 9.8346 x 10-28 kg/nucleus

ΔE = Δmc2

ΔE = (9.8346 x 10-28 kg/nucleus) x (2.9979 x 108 m/s)2 = 8.8387 x 10-11 J/nucleus

The energy calculated in the previous example is the nuclear binding energy.  However, the nuclear binding energy may be expressed as kJ/mol (for better understanding).

Calculate the nuclear binding energy of 1 mole of 63Cu:

(8.8387 x 10-11 J/nucleus) x (1 kJ/1000 J) x (6.022 x 1023 nuclei/mol) = 5.3227 x 1010 kJ/mol of nuclei.

One mole of 63Cu (~63 grams) is bound by the nuclear binding energy (5.3227 x 1010 kJ/mol) which is equivalent to:

  • 14.8 million kilowatt-hours (≈ 15 GW·h)
  • 336,100 US gallons of automotive gasoline
Example: Mass defect of the reactor core
Calculate the mass defect of the 3000MWth reactor core after one year of operation.

It is known the average recoverable energy per fission is about 200 MeV, being the total energy minus the energy of the energy of antineutrinos that are radiated away.

The reaction rate per entire 3000MWth reactor core is about  9.33×1019 fissions / second.

The overall energy release in the units of joules is:

200×106 (eV) x 1.602×10-19 (J/eV) x 9.33×1019 (s-1) x 31.5×106 (seconds in year) = 9.4×1016 J/year

The mass defect is calculated as:

Δm = ΔE/c2

Δm = 9.4×1016 / (2.9979 x 108)2 = 1.046 kg

That means in a typical 3000MWth reactor core about 1 kilogram of matter is converted into pure energy.

Note that, a typical annual uranium load for a 3000MWth reactor core is about 20 tonnes of enriched uranium (i.e. about 22.7 tonnes of UO2). Entire reactor core may contain about 80 tonnes of enriched uranium.

Mass defect directly from E=mc2

The mass defect can be calculated directly from the Einstein relationship (E = mc2) as:

Δm = ΔE/c2

Δm = 3000×106 (W = J/s) x 31.5×106 (seconds in year) / (2.9979 x 108)2 = 1.051 kg

See also:

Nuclear Energy

We hope, this article, E=mc2 Meaning, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.