Exothermic Reactions
In nuclear and particle physics the energetics of nuclear reactions is determined by the Q-value of that reaction. The Q-value of the reaction is defined as the difference between the sum of the masses of the initial reactants and the sum of the masses of the final products, in energy units (usually in MeV).
Consider a typical reaction, in which the projectile a and the target A gives place to two products, B and b. This can also be expressed in the notation that we used so far, a + A → B + b, or even in a more compact notation, A(a,b)B.
See also: E=mc2
The Q-value of this reaction is given by:
Q = [ma + mA – (mb + mB)]c2
which is the same as the excess kinetic energy of the final products:
Q = Tfinal – Tinitial
= Tb + TB – (Ta + TA)
For reactions in which there is an increase in the kinetic energy of the products Q is positive. The positive Q reactions are said to be exothermic (or exergic). There is a net release of energy, since the kinetic energy of the final state is greater than the kinetic energy of the initial state.
See also: Q-value Calculator
Example of Exothermic Reaction – Nuclear Fission
Source: hyperphysics.phy-astr.gsu.edu
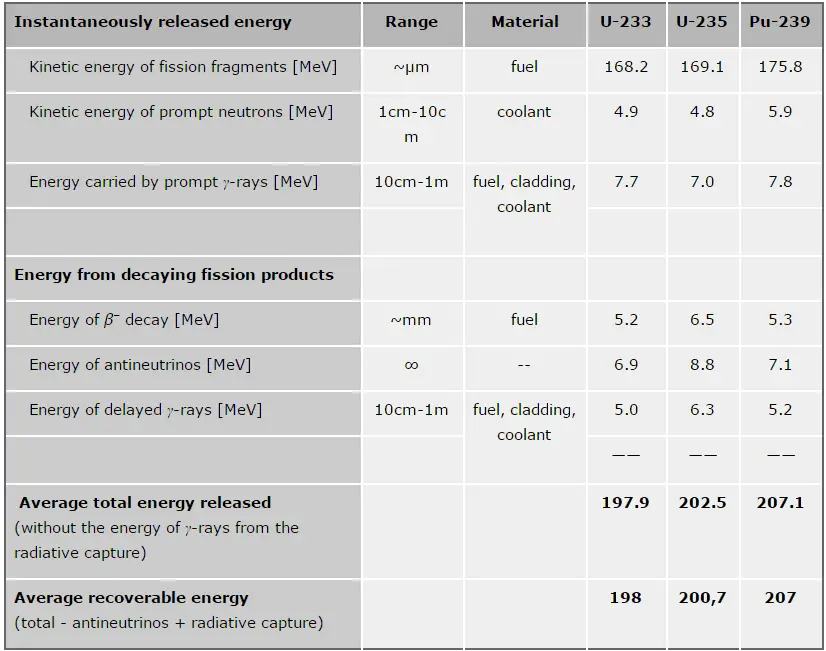
Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei). The fission process often produces free neutrons and photons (in the form of gamma rays), and releases a large amount of energy.
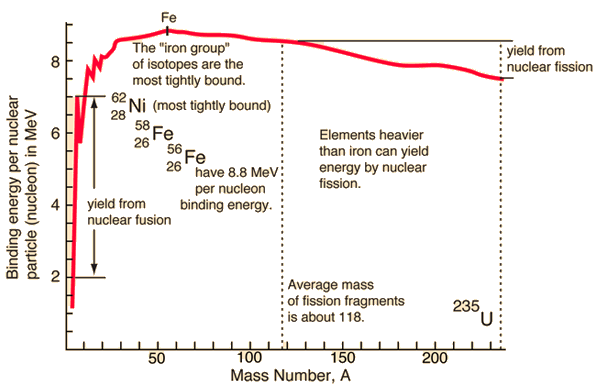
From the nuclear binding energy curve and from the table it can be seen that, in the case of splitting a 235U nucleus into two parts, the binding energy of the fragments (A ≈ 120) together is larger than that of the original 235U nucleus. According to the Weizsaecker formula, the total energy released for such reaction will be approximately 235 x (8.5 – 7.6) ≈ 200 MeV (it can also be derived from nuclear binding curve).
The total energy released in a reactor per 235U fission is distributed as shown in the table.
Example of Exothermic Reaction – DT fusion
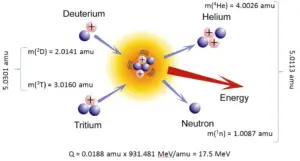
The DT fusion reaction of deuterium and tritium is particularly interesting because of its potential of providing energy for the future. Calculate the reaction Q-value.
3T (d, n) 4He
The atom masses of the reactants and products are:
m(3T) = 3.0160 amu
m(2D) = 2.0141 amu
m(1n) = 1.0087 amu
m(4He) = 4.0026 amu
Using the mass-energy equivalence, we get the Q-value of this reaction as:
Q = {(3.0160+2.0141) [amu] – (1.0087+4.0026) [amu]} x 931.481 [MeV/amu]
= 0.0188 x 931.481 = 17.5 MeV
Example of Exothermic Reaction – Tritium in Reactors
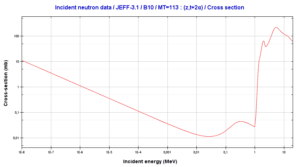
Tritium is a byproduct in nuclear reactors. Most of the tritium produced in nuclear power plants stems from the boric acid, which is commonly used as a chemical shim to compensate an excess of initial reactivity. Main reaction, in which the tritium is generated from boron is below:
10B(n,2*alpha)T
This reaction of a neutron with an isotope 10B is the main way, how radioactive tritium in primary circuit of all PWRs is generated. Note that, this reaction is a threshold reaction due to its cross-section.
Calculate the reaction Q-value.
The atom masses of the reactants and products are:
m(10B) = 10.01294 amu
m(1n) = 1.00866 amu
m(3T) = 3.01604 amu
m(4He) = 4.0026 amu
Using the mass-energy equivalence, we get the Q-value of this reaction as:
Q = {(10.0129+1.00866) [amu] – (3.01604+2 x 4.0026) [amu]} x 931.481 [MeV/amu]
= 0.00036 x 931.481 = 0.335 MeV
We hope, this article, Exothermic Reaction, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.