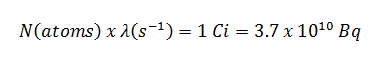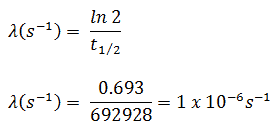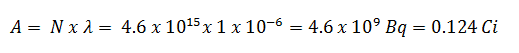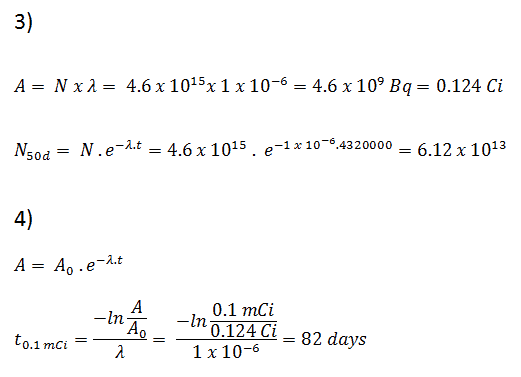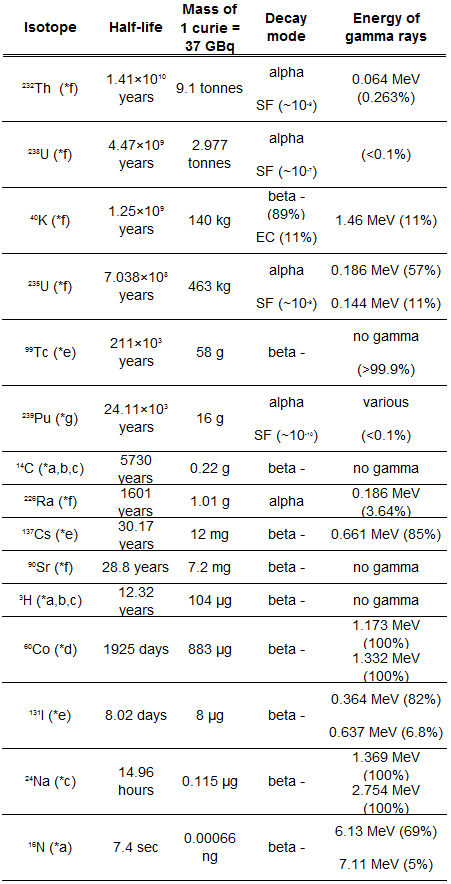 One of the most useful terms for estimating how quickly a nuclide will decay is the radioactive half-life (t1/2). The half-life is defined as the amount of time it takes for a given isotope to lose half of its radioactivity. As was written, radioactive decay is a random process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay. In other words, a nucleus of a radionuclide has no “memory”. A nucleus does not “age” with the passage of time. Thus, the probability of its breaking down does not increase with time, but stays constant no matter how long the nucleus has existed.
One of the most useful terms for estimating how quickly a nuclide will decay is the radioactive half-life (t1/2). The half-life is defined as the amount of time it takes for a given isotope to lose half of its radioactivity. As was written, radioactive decay is a random process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay. In other words, a nucleus of a radionuclide has no “memory”. A nucleus does not “age” with the passage of time. Thus, the probability of its breaking down does not increase with time, but stays constant no matter how long the nucleus has existed.
Therefore, the rate of nuclear decay can be also measured in terms of half-lives. Each radionuclide has its own particular half-life that never changes, regardless of the quantity or form of the material (i.e., solid, liquid, gas, element or compound) or its past history. If a radioisotope has a half-life of 14 days, half of its atoms will have decayed within 14 days. In 14 more days, half of that remaining half will decay, and so on.
Half lives range from millionths of a second for highly radioactive fission products to billions of years for long-lived materials (such as naturally occurring uranium). After five half-lives have elapsed, only 1/32, or 3.1%, of the original number of atoms remains. After seven half-lives, only 1/128, or 0.78%, of the atoms remains. The number of atoms existing after 5 to 7 half-lives can usually be assumed to be negligible.
Half-Life and Radioactivity – Example
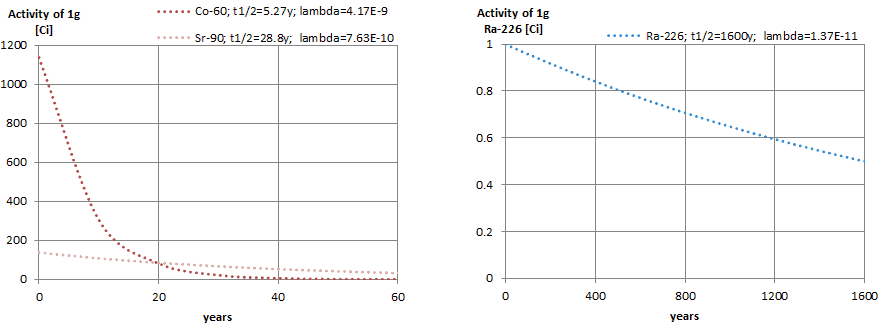
The relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown in the figure. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:
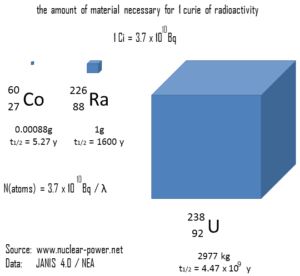 The following figure illustrates the amount of material necessary for 1 curie of radioactivity. It is obvious, that the longer the half-life, the greater the quantity of radionuclide needed to produce the same activity. Of course, the longer lived substance will remain radioactive for a much longer time. As can be seen, the amount of material necessary for 1 curie of radioactivity can vary from an amount too small to be seen (0.00088 gram of cobalt-60), through 1 gram of radium-226, to almost three tons of uranium-238.
The following figure illustrates the amount of material necessary for 1 curie of radioactivity. It is obvious, that the longer the half-life, the greater the quantity of radionuclide needed to produce the same activity. Of course, the longer lived substance will remain radioactive for a much longer time. As can be seen, the amount of material necessary for 1 curie of radioactivity can vary from an amount too small to be seen (0.00088 gram of cobalt-60), through 1 gram of radium-226, to almost three tons of uranium-238.
Example – Radioactive Decay Law
 A sample of material contains 1 mikrogram of iodine-131. Note that, iodine-131 plays a major role as a radioactive isotope present in nuclear fission products, and it a major contributor to the health hazards when released into the atmosphere during an accident. Iodine-131 has a half-life of 8.02 days.
A sample of material contains 1 mikrogram of iodine-131. Note that, iodine-131 plays a major role as a radioactive isotope present in nuclear fission products, and it a major contributor to the health hazards when released into the atmosphere during an accident. Iodine-131 has a half-life of 8.02 days.
Calculate:
- The number of iodine-131 atoms initially present.
- The activity of the iodine-131 in curies.
- The number of iodine-131 atoms that will remain in 50 days.
- The time it will take for the activity to reach 0.1 mCi.
Solution:
- The number of atoms of iodine-131 can be determined using isotopic mass as below.
NI-131 = mI-131 . NA / MI-131
NI-131 = (1 μg) x (6.02×1023 nuclei/mol) / (130.91 g/mol)
NI-131 = 4.6 x 1015 nuclei
- The activity of the iodine-131 in curies can be determined using its decay constant:
In calculations of radioactivity one of two parameters (decay constant or half-life), which characterize the rate of decay, must be known. There is a relation between the half-life (t1/2) and the decay constant λ. The relationship can be derived from decay law by setting N = ½ No. This gives:
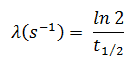 where ln 2 (the natural log of 2) equals 0.693. If the decay constant (λ) is given, it is easy to calculate the half-life, and vice-versa.
where ln 2 (the natural log of 2) equals 0.693. If the decay constant (λ) is given, it is easy to calculate the half-life, and vice-versa.
The iodine-131 has half-live of 8.02 days (692928 sec) and therefore its decay constant is:
Using this value for the decay constant we can determine the activity of the sample:
3) and 4) The number of iodine-131 atoms that will remain in 50 days (N50d) and the time it will take for the activity to reach 0.1 mCi can be calculated using the decay law:
As can be seen, after 50 days the number of iodine-131 atoms and thus the activity will be about 75 times lower. After 82 days the activity will be approximately 1200 times lower. Therefore, the time of ten half-lives (factor 210 = 1024) is widely used to define residual activity.
We hope, this article, Half-Life – Calculation – Example, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.