X-rays, also known as X-radiation, refers to electromagnetic radiation (no rest mass, no charge) of high energies. X-rays are high-energy photons with short wavelengths and thus very high frequency. The radiation frequency is key parameter of all photons, because it determines the energy of a photon. Photons are categorized according to the energies from low-energy radio waves and infrared radiation, through visible light, to high-energy X-rays and gamma rays.
Most X-rays have a wavelength ranging from 0.01 to 10 nanometers (3×1016 Hz to 3×1019 Hz), corresponding to energies in the range 100 eV to 100 keV. X-ray wavelengths are shorter than those of UV rays and typically longer than those of gamma rays. The distinction between X-rays and gamma rays is not so simple and has changed in recent decades. According to the currently valid definition, X-rays are emitted by electrons outside the nucleus, while gamma rays are emitted by the nucleus.
Half Value Layer
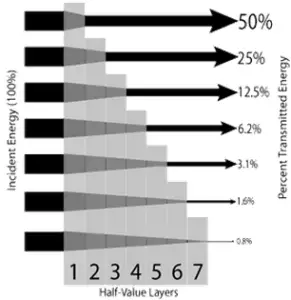 The half value layer expresses the thickness of absorbing material needed for reduction of the incident radiation intensity by a factor of two. There are two main features of the half value layer:
The half value layer expresses the thickness of absorbing material needed for reduction of the incident radiation intensity by a factor of two. There are two main features of the half value layer:
- The half value layer decreases as the atomic number of the absorber increases. For example 35 m of air is needed to reduce the intensity of a 100 keV X-ray beam by a factor of two whereas just 0.12 mm of lead can do the same thing.
- The half value layer for all materials increases with the energy of the X-rays. For example from 0.26 cm for iron at 100 keV to about 0.64 cm at 200 keV.
Half Value Layer – Example:
How much water schielding do you require, if you want to reduce the intensity of a 100 keV monoenergetic X-ray beam (narrow beam) to 1% of its incident intensity? The half value layer for 100 keV X-rays in water is 4.15 cm and the linear attenuation coefficient for 100 keV X-rays in water is 0.167 cm-1. The problem is quite simple and can be described by following equation:
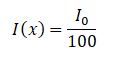 If the half value layer for water is 4.15 cm, the linear attenuation coefficient is:
If the half value layer for water is 4.15 cm, the linear attenuation coefficient is: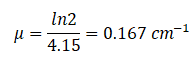 Now we can use the exponential attenuation equation:
Now we can use the exponential attenuation equation:
So the required thickness of water is about 27.58 cm. This is relatively large thickness and it is caused by small atomic numbers of hydrogen and oxygen. If we calculate the same problem for lead (Pb), we obtain the thickness x=0.077 cm.
Half Value Layers
Table of Half Value Layers (in cm) for a different materials at photon energies of 100, 200 and 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Air | 3555 cm | 4359 cm | 6189 cm |
| Water | 4.15 cm | 5.1 cm | 7.15 cm |
| Carbon | 2.07 cm | 2.53 cm | 3.54 cm |
| Aluminium | 1.59 cm | 2.14 cm | 3.05 cm |
| Iron | 0.26 cm | 0.64 cm | 1.06 cm |
| Copper | 0.18 cm | 0.53 cm | 0.95 cm |
| Lead | 0.012 cm | 0.068 cm | 0.42 cm |
We hope, this article, Half Value Layer – X-rays, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.