What is Wear Coefficient - Definition

Wear can be quantified (correlated) by means of wear rate, defined as the mass or volume of material removed per unit sliding distance. It is usually expressed in terms of the dimensionless wear coefficient (K) or as specific wear rate.

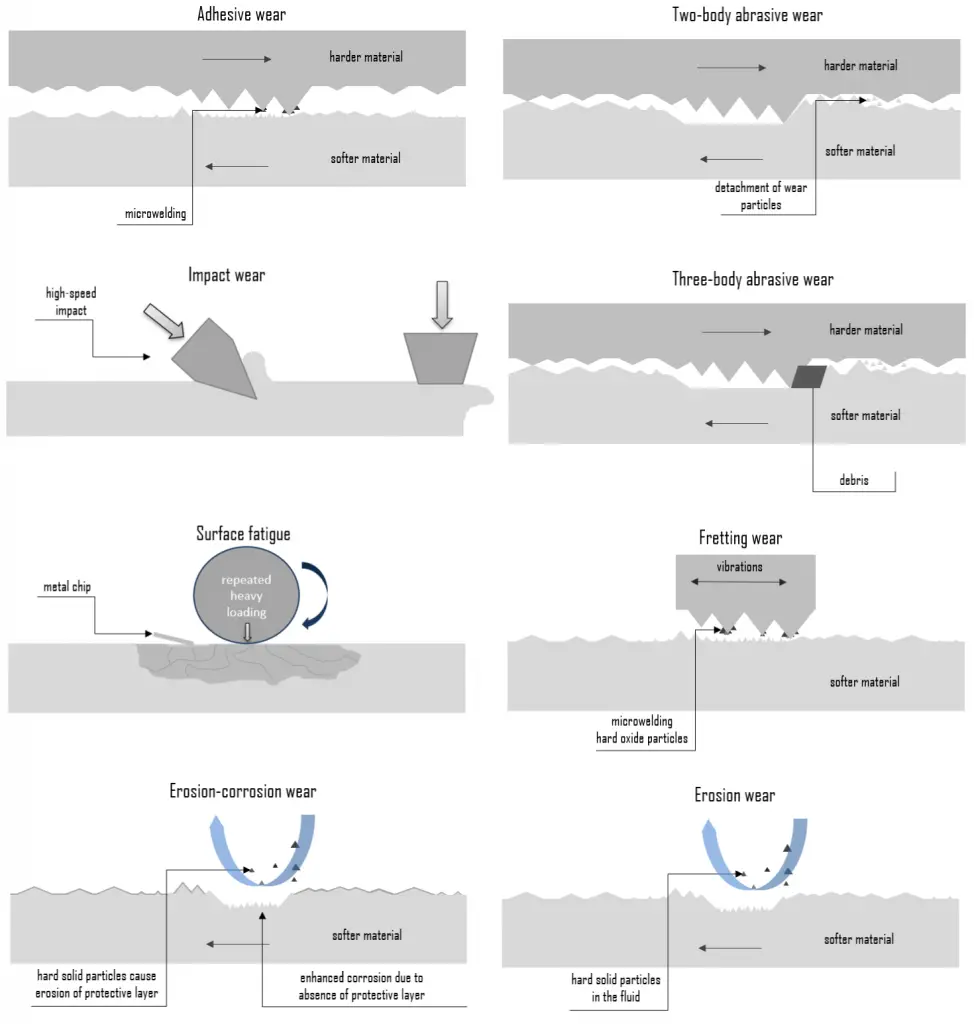
wear In general, wear is mechanically induced surface damage that results in the progressive removal of material due to relative motion between that surface and a contacting substance or substances. A contacting substance may consist of another surface, a fluid, or hard, abrasive particles contained in some form of fluid or suspension, such as a lubricant for example. As is with friction, the presence of wear can be either good or bad. Productive, controlled wear can be found in processes like machining, cutting, grinding and polishing. However, in most of the technological applications, the occurrence of wear is highly undesirable and it is an enormously expensive problem since it leads to the deterioration or even failure of components. In terms of safety it is often not as serious (or as sudden) as fracture. This is because wear is usually anticipated.

Certain material characteristics such as hardness, carbide type, and volume percent can have a decided impact on the wear resistance of a material in a given application. Wear, like corrosion, has multiple types and subtypes, is predictable to some extent, and is rather difficult to reliably test and to evaluate in the lab or in service.

Wear Coefficient

Wear can be quantified (correlated) by means of wear rate, defined as the mass or volume of material removed per unit sliding distance. It is usually expressed in terms of the dimensionless wear coefficient (K) or as specific wear rate (wear volume per unit applied normal load per unit sliding distance) in (mm³*Nm^-1).

The most commonly used wear equation for the dry rolling–sliding condition is Archards wear equation. The wear volume (V), for unit sliding distance (S) is equal to the non-dimensional wear coefficient (K) multiplied by the applied load (Fn) divided by the hardness of the worn material.

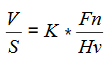
wear coefficient

References:

Materials Science:

U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 2 and 2. January 1993.
William D. Callister, David G. Rethwisch. Materials Science and Engineering: An Introduction 9th Edition, Wiley; 9 edition (December 4, 2013), ISBN-13: 978-1118324578.
Eberhart, Mark (2003). Why Things Break: Understanding the World by the Way It Comes Apart. Harmony. ISBN 978-1-4000-4760-4.
Gaskell, David R. (1995). Introduction to the Thermodynamics of Materials (4th ed.). Taylor and Francis Publishing. ISBN 978-1-56032-992-3.
González-Viñas, W. & Mancini, H.L. (2004). An Introduction to Materials Science. Princeton University Press. ISBN 978-0-691-07097-1.
Ashby, Michael; Hugh Shercliff; David Cebon (2007). Materials: engineering, science, processing and design (1st ed.). Butterworth-Heinemann. ISBN 978-0-7506-8391-3.
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.

See above:
Wear

We hope, this article, Wear Coefficient, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.