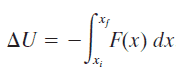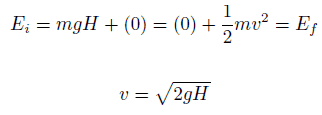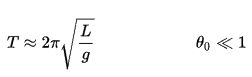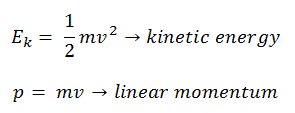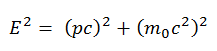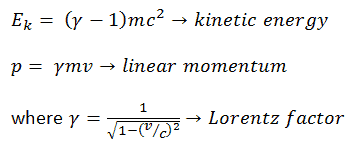What is Kinetic Energy
The kinetic energy, K, is defined as the energy stored in an object because of its motion. An object in motion has the ability to do work and thus can be said to have energy. It is called kinetic energy, from the Greek word kinetikos, meaning “motion.”
The kinetic energy depends on the speed of an object and is the ability of a moving object to do work on other objects when it collides with them. On the other hand, the kinetic energy of an object represents the amount of energy required to increase the velocity of the object from rest (v = 0) to its final velocity. The kinetic energy also depends linearly on the mass, which is a numerical measure of object’s inertia and the measure of an object’s resistance to acceleration when a force is applied.
We define the quantity:
K = ½ mv2
to be the translational kinetic energy of the object. It must be added, it is called the “translational” kinetic energy to distinguish it from rotational kinetic energy.
Conservation of Mechanical Energy
First the principle of the Conservation of Mechanical Energy was stated:
The total mechanical energy (defined as the sum of its potential and kinetic energies) of a particle being acted on by only conservative forces is constant.
See also: Conservation of Mechanical Energy
An isolated system is one in which no external force causes energy changes. If only conservative forces act on an object and U is the potential energy function for the total conservative force, then
Emech = U + K
The potential energy, U, depends on the position of an object subjected to a conservative force.
It is defined as the object’s ability to do work and is increased as the object is moved in the opposite direction of the direction of the force.
The potential energy associated with a system consisting of Earth and a nearby particle is gravitational potential energy.
The kinetic energy, K, depends on the speed of an object and is the ability of a moving object to do work on other objects when it collides with them.
K = ½ mv2
The above mentioned definition (Emech = U + K) assumes that the system is free of friction and other non-conservative forces. The difference between a conservative and a non-conservative force is that when a conservative force moves an object from one point to another, the work done by the conservative force is independent of the path.
In any real situation, frictional forces and other non-conservative forces are present, but in many cases their effects on the system are so small that the principle of conservation of mechanical energy can be used as a fair approximation. For example the frictional force is a non-conservative force, because it acts to reduce the mechanical energy in a system.
Note that non-conservative forces do not always reduce the mechanical energy. A non-conservative force changes the mechanical energy, there are forces that increase the total mechanical energy, like the force provided by a motor or engine, is also a non-conservative force.
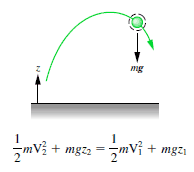
Block sliding down a frictionless incline slope
The 1 kg block starts out a height H (let say 1 m) above the ground, with potential energy mgH and kinetic energy that is equal to 0. It slides to the ground (without friction) and arrives with no potential energy and kinetic energy K = ½ mv2. Calculate the velocity of the block on the ground and its kinetic energy.
Emech = U + K = const
=> ½ mv2 = mgH
=> v = √2gH = 4.43 m/s
=> K2 = ½ x 1 kg x (4.43 m/s)2 = 19.62 kg.m2.s-2 = 19.62 J
Pendulum
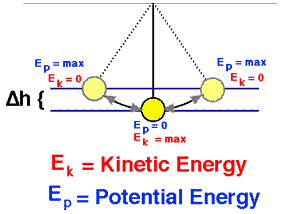 Assume a pendulum (ball of mass m suspended on a string of length L that we have pulled up so that the ball is a height H < L above its lowest point on the arc of its stretched string motion. The pendulum is subjected to the conservative gravitational force where frictional forces like air drag and friction at the pivot are negligible.
Assume a pendulum (ball of mass m suspended on a string of length L that we have pulled up so that the ball is a height H < L above its lowest point on the arc of its stretched string motion. The pendulum is subjected to the conservative gravitational force where frictional forces like air drag and friction at the pivot are negligible.
We release it from rest. How fast is it going at the bottom?
The pendulum reaches greatest kinetic energy and least potential energy when in the vertical position, because it will have the greatest speed and be nearest the Earth at this point. On the other hand, it will have its least kinetic energy and greatest potential energy at the extreme positions of its swing, because it has zero speed and is farthest from Earth at these points.
If the amplitude is limited to small swings, the period T of a simple pendulum, the time taken for a complete cycle, is:
where L is the length of the pendulum and g is the local acceleration of gravity. For small swings the period of swing is approximately the same for different size swings. That is, the period is independent of amplitude.
Relativistic Kinetic Energy
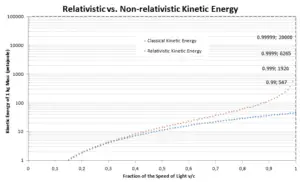
The previous relationship between work and kinetic energy are based on Newton’s laws of motion. When we generalize these laws according to the principle of relativity, we need a corresponding generalization of the equation for kinetic energy. If an object’s speed is close to the speed of light, it is necessary to use relativistic mechanics to calculate its kinetic energy.
In classical mechanics, kinetic energy and momentum are expressed as:
Derivation of its relativistic relationships is based on the relativistic energy-momentum relation:
It can be derived, the relativistic kinetic energy and the relativistic momentum are:
The first term (ɣmc2) of the relativistic kinetic energy increases with the speed v of the particle. The second term (mc2) is constant; it is called the rest energy (rest mass) of the particle, and represents a form of energy that a particle has even when at zero velocity. As velocity of an object approaches the speed of light, the kinetic energy approaches infinity. It is caused by the Lorentz factor, which approaches infinity for v → c. Therefore the speed of light cannot be reached by any massive particles.
The first term (ɣmc2) is known as the total energy E of the particle, because it equals the rest energy plus the kinetic energy:
E = K + mc2
For a particle at rest, i.e. K is zero, so the total energy is its rest energy:
E = mc2
This is one of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible one into the other. Equivalence of the mass and energy is described by Einstein’s famous formula E = mc2. This result have been experimentally confirmed countless times in nuclear and elementary particle physics. For example, see Positron-electron Pair Production or Conservation of Energy in Nuclear Reactions.
See also: thermodynamics/thermodynamic-properties/what-is-mass-and-weight/relativistic-mass-2/”>Relativistic Mass
Example: Proton’s kinetic energy
 A proton (m = 1.67 x 10-27 kg) travels at a speed v = 0.9900c = 2.968 x 108m/s. What is its kinetic energy?
A proton (m = 1.67 x 10-27 kg) travels at a speed v = 0.9900c = 2.968 x 108m/s. What is its kinetic energy?
According to a classical calculation, which is not correct, we would obtain:
K = 1/2mv2 = ½ x (1.67 x 10-27 kg) x (2.968 x 108m/s)2 = 7.355 x 10-11 J
With relativistic correction the relativistic kinetic energy is equal to:
K = (ɣ – 1)mc2
where the Lorentz factor
ɣ = 7.089
therefore
K = 6.089 x (1.67 x 10-27 kg) x (2.9979 x 108m/s)2 = 9.139 x 10-10 J = 5.701 GeV
This is about 12 times higher energy as in the classical calculation. According to this relationship, an acceleration of a proton beam to 5.7 GeV requires energies that are in the order different.
We hope, this article, Kinetic Energy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.