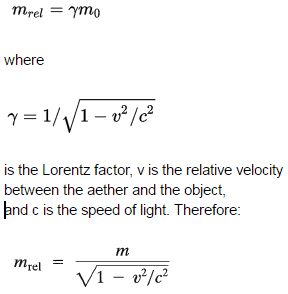Mass and Weight
One of the most familiar forces is the weight of a body, which is the gravitational force that the earth exerts on the body. In general, gravitation is a natural phenomenon by which all things with mass are brought toward one another. The terms mass and weight are often confused with one another, but it is important to distinguish between them. It is absolutely essential to understand clearly the distinctions between these two physical quantities.
See also: Law of Conservation of Mass
The mass of a certain body will remain constant even if the gravitational acceleration acting upon that body changes. For example, on earth an object has a certain mass and a certain weight. When the same object is placed in outer space, away from the earth’s gravitational field, its mass remains the same, but it is now in a “weightless” condition. This means in this condition it will weight zero, because gravitational acceleration and, thus, force will equal to zero.
Mass and weight are related: Bodies having large mass also have large weight. A large stone is hard to throw because of its large mass, and hard to lift off the ground because of its large weight. To understand the relationship between mass and weight, consider a freely falling stone, that has an acceleration of magnitude g (g = 9.81 m/s2 is the acceleration due to Earth’s gravitational field). Newton’s second law tells us that a force must act to produce this acceleration. If a 1 kilogram stone falls with an acceleration of the required force has magnitude:
F = ma = 1 [kg] x 9.81 [m/s2] = 9.8 [kg m/s2] = 9.8 N
The force that makes the body accelerate downward is its weight. Any body near the surface of the earth that has a mass of 1 kg must have a weight of 9.8 N to give it the acceleration we observe when it is in free fall.
Example: The weight of a stone on the Earth, on the Mars and on the Moon
Weight of a stone on the Earth
 The acceleration due to Earth’s gravitational field is gEarth = 9.81 m/s2.The weight of a stone with mass 1 kg on the Earth can be calculated as:
The acceleration due to Earth’s gravitational field is gEarth = 9.81 m/s2.The weight of a stone with mass 1 kg on the Earth can be calculated as:
FEarth = 1 [kg] x 9.81 [m/s2] = 9.8 [kg m/s2] = 9.8 N
Weight of a stone on the Mars
The acceleration of gravity on the Mars is approximately 38% of the acceleration of gravity on the earth. The acceleration due to Moon’s gravitational field is gMars = 3.71 m/s2.
Therefore the weight of the same stone with mass 1 kg on the Mars is:
FMoon = 1 [kg] x 3.71 [m/s2] = 3.71 [kg m/s2] = 3.71 N
Weight of a stone on the Moon
The acceleration of gravity on the Moon is approximately 1/6 of the acceleration of gravity on the earth. The acceleration due to Moon’s gravitational field is gMoon = 1.62 m/s2.
Therefore the weight of the same stone with mass 1 kg on the Moon is:
FMoon = 1 [kg] x 1.62 [m/s2] = 1.62 [kg m/s2] = 1.62 N
The Standard Kilogram
The usual symbol for mass is m and its SI unit is the kilogram. The SI standard of mass is a cylinder of platinum and iridium that is kept at the International Bureau of Weights and Measures near Paris and assigned, by international agreement, a mass of 1 kilogram.

Relativistic Mass
While the mass is normally considered to be an unchanging property of an object, at speeds approaching the speed of light one must consider the increase in the relativistic mass. The relativistic definition of momentum is sometimes interpreted as an increase in the mass of an object. In this interpretation, a particle can have a relativistic mass, mrel. The increase in effective mass with speed is given by the expression:
In this “mass-increase” formula, m is referred to as the rest mass of the object. It follows from this formula, that an object with nonzero rest mass cannot travel at the speed of light. As the object approaches the speed of light, the object’s momentum increase without bound. On the other hand, when the relative velocity is zero, the Lorentz factor is simply equal to 1, and the relativistic mass is reduced to the rest mass. With this interpretation, the mass of an object appears to increase as its speed increases. In must be added, many physicists believe an object has only one mass (its rest mass), and that it is only the momentum that increases with speed.
In special theory of relativity certain types of matter may be created or destroyed, but in all of these processes, the mass and energy associated with such matter remains unchanged in quantity. It was found the rest mass of an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E=mc2), this binding energy is proportional to this mass difference and it is known as the mass defect.
The mass of an object is a fundamental property of the object. It is a numerical measure of its inertia and the measure of an object’s resistance to acceleration when a force is applied. It is also a fundamental measure of the amount of matter in the object. The greater the mass, the greater the force needed to cause a given acceleration. This is reflected in Newton’s second law (F=ma).
The mass of a certain body will remain constant even if the gravitational acceleration acting upon that body changes. For example, on earth an object has a certain mass and a certain weight. When the same object is placed in outer space, away from the earth’s gravitational field, its mass remains the same, but it is now in a “weightless” condition. This means in this condition it will weight zero, because gravitational acceleration and, thus, force will equal to zero.
Mass and weight are related:
Bodies having large mass also have large weight. A large stone is hard to throw because of its large mass, and hard to lift off the ground because of its large weight. To understand the relationship between mass and weight, consider a freely falling stone, that has an acceleration of magnitude g (g = 9.81 m/s2 is the acceleration due to Earth’s gravitational field). Newton’s second law tells us that a force must act to produce this acceleration. If a 1 kilogram stone falls with an acceleration of the required force has magnitude:
F = ma = 1 [kg] x 9.81 [m/s2] = 9.8 [kg m/s2] = 9.8 N
The force that makes the body accelerate downward is its weight. Any body near the surface of the earth that has a mass of 1 kg must have a weight of 9.8 N to give it the acceleration we observe when it is in free fall.
Example: The weight of a stone on the Earth, on the Mars and on the Moon
Weight of a stone on the Earth
 The acceleration due to Earth’s gravitational field is gEarth = 9.81 m/s2.The weight of a stone with mass 1 kg on the Earth can be calculated as:
The acceleration due to Earth’s gravitational field is gEarth = 9.81 m/s2.The weight of a stone with mass 1 kg on the Earth can be calculated as:
FEarth = 1 [kg] x 9.81 [m/s2] = 9.8 [kg m/s2] = 9.8 N
Weight of a stone on the Mars
The acceleration of gravity on the Mars is approximately 38% of the acceleration of gravity on the earth. The acceleration due to Moon’s gravitational field is gMars = 3.71 m/s2.
Therefore the weight of the same stone with mass 1 kg on the Mars is:
FMoon = 1 [kg] x 3.71 [m/s2] = 3.71 [kg m/s2] = 3.71 N
Weight of a stone on the Moon
The acceleration of gravity on the Moon is approximately 1/6 of the acceleration of gravity on the earth. The acceleration due to Moon’s gravitational field is gMoon = 1.62 m/s2.
Therefore the weight of the same stone with mass 1 kg on the Moon is:
FMoon = 1 [kg] x 1.62 [m/s2] = 1.62 [kg m/s2] = 1.62 N
Principle of Equivalence:
An observer cannot determine, in any way whatsoever, whether the laboratory he occupies is in a uniform gravitational field or is in a reference frame that is accelerating relative to an inertial frame.
This led to an ambiguity as to what exactly is meant by the force of gravity and weight. A scale in an accelerating elevator cannot be distinguished from a scale in a gravitational field. Gravitational force and weight thereby became essentially frame-dependent quantities. According to the general theory of relativity, gravitational and inertial mass are not different properties of matter but two aspects of a fundamental and single property of matter.
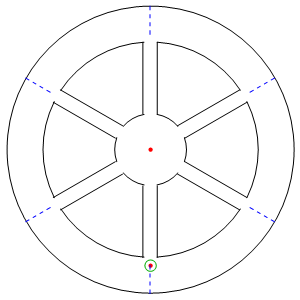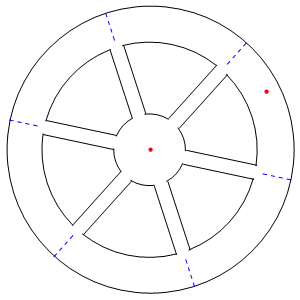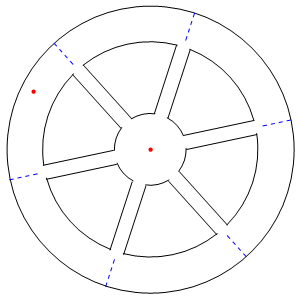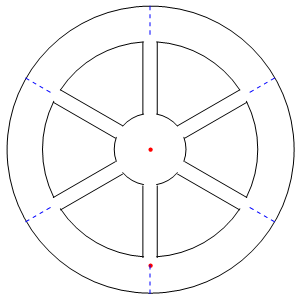
In situations in which gravitation is absent but the chosen coordinate system is not inertial, but is accelerated with the observer, then g-forces and corresponding proper accelerations felt by observers in these coordinate systems are caused by the mechanical forces which resist their weight in such systems. The most realistic method of producing artificial gravity, for example aboard a space station, can be imitated in a rotating spaceship. Objects inside would be pushed toward the hull and they will have some weight. This weight is produced by fictitious forces or “inertial forces” which appear in all such accelerated coordinate systems. Unlike real gravity, which pulls towards a center of the planet, the centripetal force pushes towards the axis of rotation.
- J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
- J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
- Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
- Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
- Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
- Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
- Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
- U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.
We hope, this article, Mass and Weight – Properties, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.