Units of Entropy
The SI unit for entropy is J/K. According to Clausius, the entropy was defined via the change in entropy S of a system. The change in entropy S, when an amount of heat Q is added to it by a reversible process at constant temperature, is given by:
Here Q is the energy transferred as heat to or from the system during the process, and T is the temperature of the system in kelvins during the process. If we assume a reversible isothermal process, the total entropy change is given by:
∆S = S2 – S1 = Q/T
In this equation the quotient Q/T is related to the increase in disorder. Higher temperature means greater randomness of motion. At lower temperatures adding heat Q causes a substantial fractional increase in molecular motion and randomness. On the other hand if the substance is already hot, the same quantity of heat Q adds relatively little to the greater molecular motion.
Example: Entropy change in melting ice
Calculate the change in entropy of 1 kg of ice at 0°C, when melted reversibly to water at 0°C.
Since it is an isothermal process, we can use:
∆S = S2 – S1 = Q/T
therefore the entropy change will be:
∆S = 334 [kJ] / 273.15 [K] = 1.22 [kJ/K]
where 334 kilojoules of heat are required to melt 1 kg of ice (latent heat of fusion = 334 kJ/kg) and this heat is transferred to the system at 0°C (273.15 K).
Specific Entropy
The entropy can be made into an intensive, or specific, variable by dividing by the mass. Engineers use the specific entropy in thermodynamic analysis more than the entropy itself. The specific entropy (s) of a substance is its entropy per unit mass. It equals to the total entropy (S) divided by the total mass (m).
s = S/m
where:
s = specific entropy (J/kg)
S = entropy (J)
m = mass (kg)
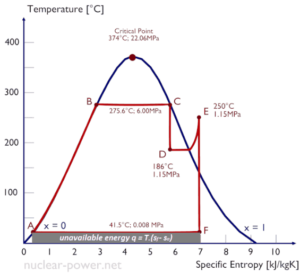
Entropy quantifies the energy of a substance that is no longer available to perform useful work. Because entropy tells so much about the usefulness of an amount of heat transferred in performing work, the steam tables include values of specific entropy (s = S/m) as part of the information tabulated.
In general, specific entropy is a property of a substance, like pressure, temperature, and volume, but it cannot be measured directly. Normally, the entropy of a substance is given with respect to some reference value. For example, the specific entropy of water or steam is given using the reference that the specific entropy of water is zero at 0.01°C and normal atmospheric pressure, where s = 0.00 kJ/kg. The fact that the absolute value of specific entropy is unknown is not a problem, however, because it is the change in specific entropy (∆s) and not the absolute value that is important in practical problems.
We hope, this article, Unit of Entropy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about materials and their properties.
