Alliage 6061 – Densité – Résistance – Dureté – Point de fusion

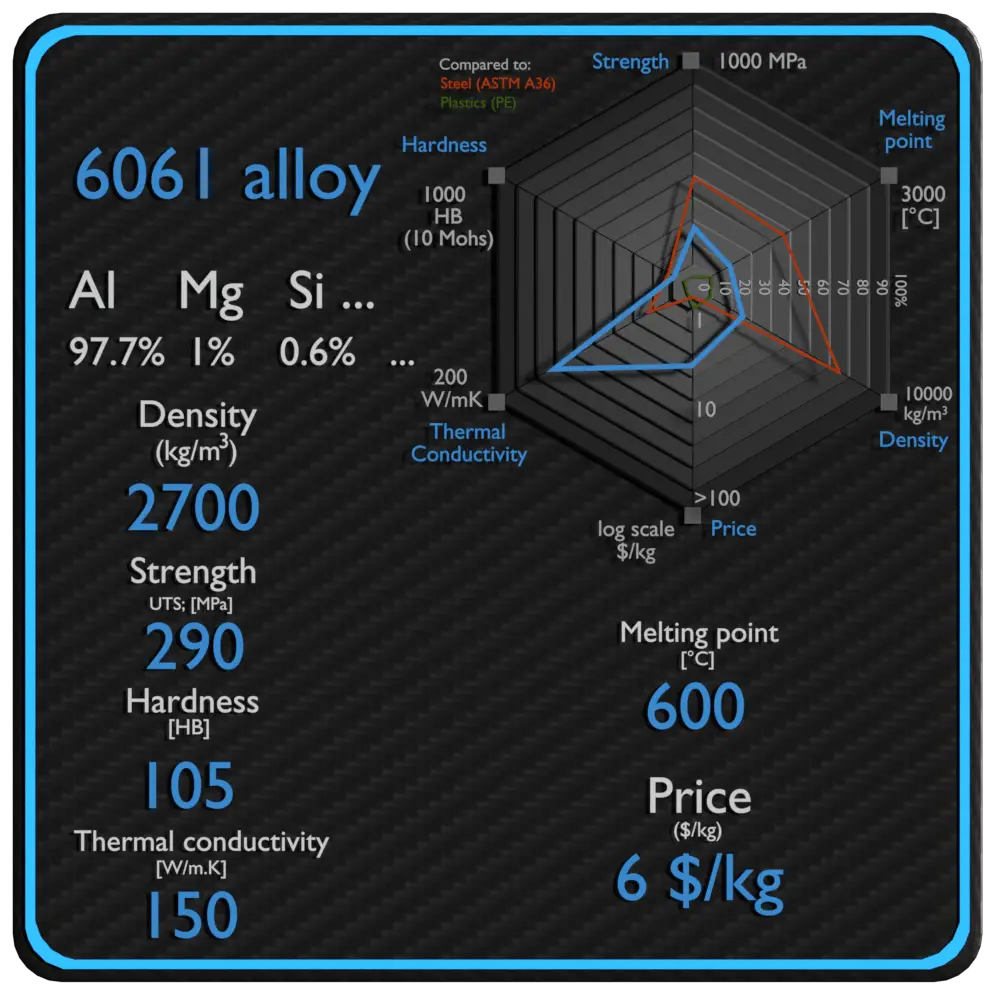
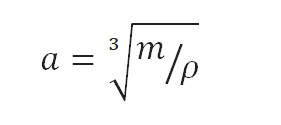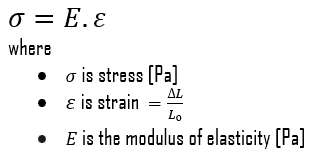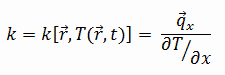À propos de l’alliage 6061

En général, les alliages d’aluminium de la série 6000 sont alliés au magnésium et au silicium. L’alliage 6061 est l’un des alliages les plus utilisés de la série 6000. Il a de bonnes propriétés mécaniques, il est facile à usiner, il est soudable et peut être durci par précipitation, mais pas aux résistances élevées que 2000 et 7000 peuvent atteindre. Il a une très bonne résistance à la corrosion et une très bonne soudabilité bien qu’une résistance réduite dans la zone de soudure. Les propriétés mécaniques du 6061 dépendent fortement de la trempe ou du traitement thermique du matériau. Par rapport à l’alliage 2024, le 6061 est plus facile à travailler et reste résistant à la corrosion même lorsque la surface est abrasée.

Cet alliage structurel standard, l’un des plus polyvalents des alliages pouvant être traités thermiquement, est populaire pour les exigences de résistance moyenne à élevée et possède de bonnes caractéristiques de ténacité. Les applications vont des composants d’avions (structures d’avions, telles que les ailes et les fuselages) aux pièces automobiles telles que le châssis de l’Audi A8. Le 6061-T6 est largement utilisé pour les cadres et composants de vélo.

Résumé

Nom	Alliage 6061
Phase à STP	solide
Densité	2700kg/m3
Résistance à la traction ultime	290 MPa
Limite d’élasticité	240 MPa
Module de Young	69 GPa
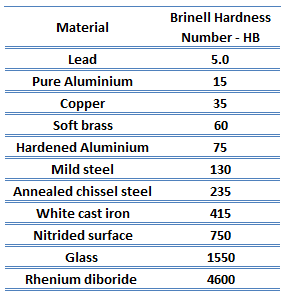
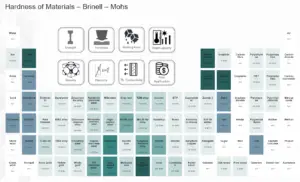
Dureté Brinell	105 BHN
Point de fusion	600 °C
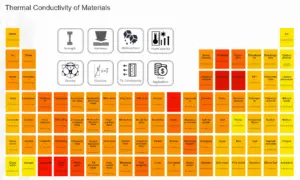
Conductivité thermique	150W/mK
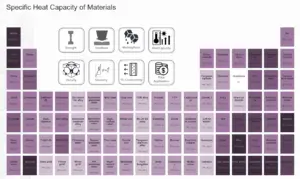
Capacité thermique	896 J/g·K
Prix	6 $/kg

Densité de l’alliage 6061

Les densités typiques de diverses substances sont à la pression atmosphérique. La densité est définie comme la masse par unité de volume. C’est une  propriété intensive, qui est définie mathématiquement comme la masse divisée par le volume: ρ = m/V

En d’autres termes, la densité (ρ) d’une substance est la masse totale (m) de cette substance divisée par le volume total (V) occupé par cette substance. L’unité SI standard est le kilogramme par mètre cube (kg/m³). L’unité anglaise standard est la masse de livres par pied cube (lbm/ft³).

La densité de l’alliage 6061 est de 2700 kg/m³.

Exemple: Densité

Calculez la hauteur d’un cube en alliage 6061, qui pèse une tonne métrique.

Solution:

La densité est définie comme la masse par unité de volume. Il est mathématiquement défini comme la masse divisée par le volume: ρ = m/V

Comme le volume d’un cube est la troisième puissance de ses côtés (V = a ³ ), la hauteur de ce cube peut être calculée:

La hauteur de ce cube est alors a = 0,718 m.

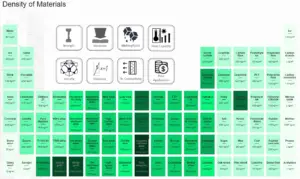
Propriétés mécaniques du carbure de bore

Résistance de l’alliage 6061

En mécanique des matériaux, la résistance d’un matériau est sa capacité à supporter une charge appliquée sans rupture ni déformation plastique. La résistance des matériaux considère essentiellement la relation entre les charges externes appliquées à un matériau et la déformation ou la modification des dimensions du matériau qui en résulte. La résistance d’un matériau est sa capacité à supporter cette charge appliquée sans défaillance ni déformation plastique.

Résistance à la traction ultime

La résistance à la traction ultime de l’alliage d’aluminium 6061 dépend fortement de l’état du matériau, mais pour l’état T6, elle est d’environ 290 MPa.

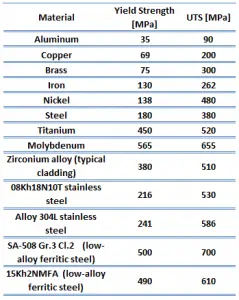La résistance à la traction ultime est le maximum sur la courbe technique de contrainte-déformation. Cela correspond à la contrainte maximalequi peut être soutenu par une structure en tension. La résistance à la traction ultime est souvent abrégée en « résistance à la traction » ou même en « l’ultime ». Si cette contrainte est appliquée et maintenue, une fracture en résultera. Souvent, cette valeur est nettement supérieure à la limite d’élasticité (jusqu’à 50 à 60 % de plus que le rendement pour certains types de métaux). Lorsqu’un matériau ductile atteint sa résistance ultime, il subit une striction où la section transversale se réduit localement. La courbe contrainte-déformation ne contient pas de contrainte supérieure à la résistance ultime. Même si les déformations peuvent continuer à augmenter, la contrainte diminue généralement après que la résistance ultime a été atteinte. C’est une propriété intensive; sa valeur ne dépend donc pas de la taille de l’éprouvette. Cependant, cela dépend d’autres facteurs, tels que la préparation de l’échantillon, température de l’environnement et du matériau d’essai. Les résistances ultimes à la traction varient de 50 MPa pour un aluminium jusqu’à 3000 MPa pour les aciers à très haute résistance.

Limite d’élasticité

La limite d’élasticité de l’alliage d’aluminium 6061 dépend fortement de l’état du matériau, mais pour l’état T6, elle est d’environ 240 MPa.

La limite d’ élasticité est le point sur une courbe contrainte-déformation qui indique la limite du comportement élastique et le début du comportement plastique. Limite d’élasticitéou la limite d’élasticité est la propriété du matériau définie comme la contrainte à laquelle un matériau commence à se déformer plastiquement, tandis que la limite d’élasticité est le point où la déformation non linéaire (élastique + plastique) commence. Avant la limite d’élasticité, le matériau se déforme élastiquement et reprend sa forme d’origine lorsque la contrainte appliquée est supprimée. Une fois la limite d’élasticité dépassée, une partie de la déformation sera permanente et irréversible. Certains aciers et autres matériaux présentent un comportement appelé phénomène de limite d’élasticité. Les limites d’élasticité varient de 35 MPa pour un aluminium à faible résistance à plus de 1400 MPa pour les aciers à très haute résistance.

Module de Young

Le module d’élasticité de Young de l’alliage d’aluminium 6061 est d’environ 69 GPa.

Le module de Young est le module d’élasticité pour les contraintes de traction et de compression dans le régime d’élasticité linéaire d’une déformation uniaxiale et est généralement évalué par des essais de traction. Jusqu’à une contrainte limite, une caisse pourra retrouver ses dimensions au retrait de la charge. Les contraintes appliquées font que les atomes d’un cristal se déplacent de leur position d’équilibre. Tous les atomes sont déplacés de la même quantité et conservent toujours leur géométrie relative. Lorsque les contraintes sont supprimées, tous les atomes reviennent à leur position d’origine et aucune déformation permanente ne se produit. Selon la loi de Hooke, la contrainte est proportionnelle à la déformation (dans la région élastique), et la pente est le module de Young. Le module de Young est égal à la contrainte longitudinale divisée par la déformation.

Dureté de l’alliage 6061

La dureté Brinell de l’alliage d’aluminium 6061 dépend fortement de l’état du matériau, mais pour l’état T6, elle est d’environ 105 MPa.

Le test de dureté Rockwell est l’un des tests de dureté par indentation les plus courants, qui a été développé pour les tests de dureté. Contrairement au test Brinell, le testeur Rockwell mesure la profondeur de pénétration d’un pénétrateur sous une charge importante (charge majeure) par rapport à la pénétration faite par une précharge (charge mineure). La charge mineure établit la position zéro. La charge majeure est appliquée, puis retirée tout en maintenant la charge mineure. La différence entre la profondeur de pénétration avant et après l’application de la charge principale est utilisée pour calculer le  nombre de dureté Rockwell . C’est-à-dire que la profondeur de pénétration et la dureté sont inversement proportionnelles. Le principal avantage de la dureté Rockwell est sa capacité à  afficher directement les valeurs de dureté. Le résultat est un nombre sans dimension noté  HRA, HRB, HRC , etc., où la dernière lettre est l’échelle Rockwell respective.

Le test Rockwell C est réalisé avec un pénétrateur Brale (cône diamant 120°) et une charge majeure de 150kg.

Exemple: Force

Supposons une tige en plastique, qui est faite d’alliage 6061. Cette tige en plastique a une section transversale de 1 cm². Calculez la force de traction nécessaire pour atteindre la résistance ultime à la traction de ce matériau, soit: UTS = 290 MPa.

Solution:

La contrainte (σ) peut être assimilée à la charge par unité de surface ou à la force (F) appliquée par section transversale (A) perpendiculaire à la force comme suit:

par conséquent, la force de traction nécessaire pour atteindre la résistance à la traction ultime est:

F = UTS x A = 290 x 10⁶ x 0,0001 = 29 000 N

Propriétés thermiques de l’alliage 6061

Les propriétés thermiques des matériaux font référence à la réponse des matériaux aux changements de thermodynamics/thermodynamic-properties/what-is-temperature-physics/ »>température et à l’application de chaleur. Lorsqu’un solide absorbe de thermodynamics/what-is-energy-physics/ »>l’énergie sous forme de chaleur, sa température augmente et ses dimensions augmentent. Mais différents matériaux réagissent différemment à l’application de chaleur.

La capacité calorifique, la dilatation thermique et la conductivité thermique sont des propriétés souvent critiques dans l’utilisation pratique des solides.

Point de fusion de l’alliage 6061

Le point de fusion de l’alliage d’aluminium 6061 est d’environ 600°C.

En général, la fusion est un  changement de phase d’une substance de la phase solide à la phase liquide. Le point de fusion d’une substance est la température à laquelle ce changement de phase se produit. Le point de fusion définit également une condition dans laquelle le solide et le liquide peuvent exister en équilibre.

Conductivité thermique de l’alliage 6061

La conductivité thermique de l’alliage d’aluminium 6061 est de 150 W/(mK).

Les caractéristiques de transfert de chaleur d’un matériau solide sont mesurées par une propriété appelée la conductivité thermique, k (ou λ), mesurée en  W/mK. C’est une mesure de la capacité d’une substance à transférer de la chaleur à travers un matériau par  conduction. Notez que la loi de Fourier s’applique à toute matière, quel que soit son état (solide, liquide ou gazeux), par conséquent, elle est également définie pour les liquides et les gaz.

La conductivité thermique  de la plupart des liquides et des solides varie avec la température. Pour les vapeurs, cela dépend aussi de la pression. En général:

La plupart des matériaux sont presque homogènes, nous pouvons donc généralement écrire  k = k (T). Des définitions similaires sont associées aux conductivités thermiques dans les directions y et z (ky, kz), mais pour un matériau isotrope, la conductivité thermique est indépendante de la direction de transfert, kx = ky = kz = k.

Exemple: Calcul du transfert de chaleur

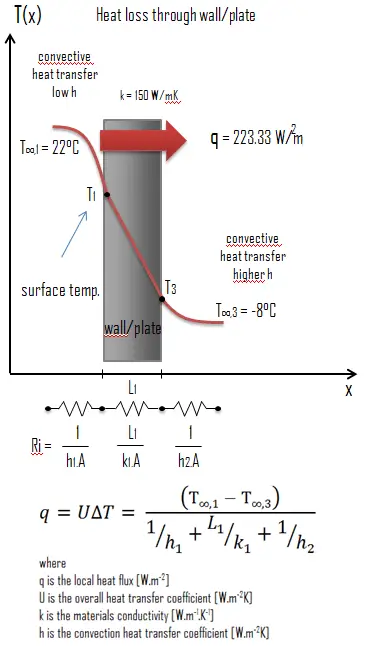La conductivité thermique est définie comme la quantité de chaleur (en watts) transférée à travers une surface carrée de matériau d’une épaisseur donnée (en mètres) en raison d’une différence de température. Plus la conductivité thermique du matériau est faible, plus la capacité du matériau à résister au transfert de chaleur est grande.

Calculer le taux de  flux de chaleur à  travers un mur de 3 mx 10 m de surface (A = 30 m ² ). Le mur a une épaisseur de 15 cm (L₁) et est en alliage 6061 avec une conductivité thermique  de k₁ = 150 W/mK (mauvais isolant thermique). Supposons que les températures intérieure et extérieure  sont de 22°C et -8°C, et que les  coefficients de transfert de chaleur par convection sur les côtés intérieur et extérieur sont h₁ = 10 W/m²K et h₂ = 30 W/m²K, respectivement. A noter que ces coefficients de convection dépendent fortement notamment des conditions ambiantes et intérieures (vent, humidité, etc.).

Calculez le flux de chaleur (perte de chaleur) à travers ce mur.

Solution:

Comme cela a été écrit, de nombreux processus de transfert de chaleur impliquent des systèmes composites et impliquent même une combinaison de conduction et de convection. Avec ces systèmes composites, il est souvent pratique de travailler avec un  coefficient de transfert de chaleur global, appelé facteur U. Le facteur U est défini par une expression analogue à  la loi de refroidissement de Newton:

Le  coefficient de transfert de chaleur global est lié à la résistance thermique totale et dépend de la géométrie du problème.

En supposant un transfert de chaleur unidimensionnel à travers la paroi plane et sans tenir compte du rayonnement, le coefficient de transfert de chaleur global peut être calculé comme suit:

Le coefficient de transfert thermique global est alors: U = 1 / (1/10 + 0,15/150 + 1/30) = 7,44 W/m²K

Le flux de chaleur peut alors être calculé simplement comme suit: q = 7,44 [W/m²K] x 30 [K] = 223,33 W/m²

La perte totale de chaleur à travers ce mur sera de: q_perte = q . A = 223,33 [W/m²] x 30 [m²] = 6699,75 W