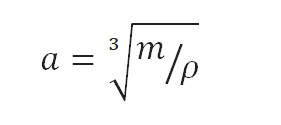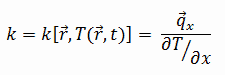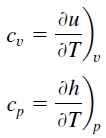Hastelloy – Densité – Résistance – Dureté – Point de fusion

À propos d’Hastelloy

Hastelloy est un superalliage forgé nickel-molybdène-chrome qui est généralement considéré comme un alliage polyvalent résistant à la corrosion. Cet alliage résiste à la formation de précipités aux joints de grains dans la zone affectée thermiquement par la soudure, ce qui le rend adapté à la plupart des applications de procédés chimiques à l’état brut de soudage. Les superalliages ont une bonne résistance à l’oxydation et au fluage et peuvent être renforcés par des méthodes de durcissement par précipitation, de durcissement en solution solide et d’écrouissage. Ils peuvent également fonctionner sous des contraintes mécaniques élevées et à des températures élevées, ainsi que dans des endroits nécessitant une grande stabilité de surface. 

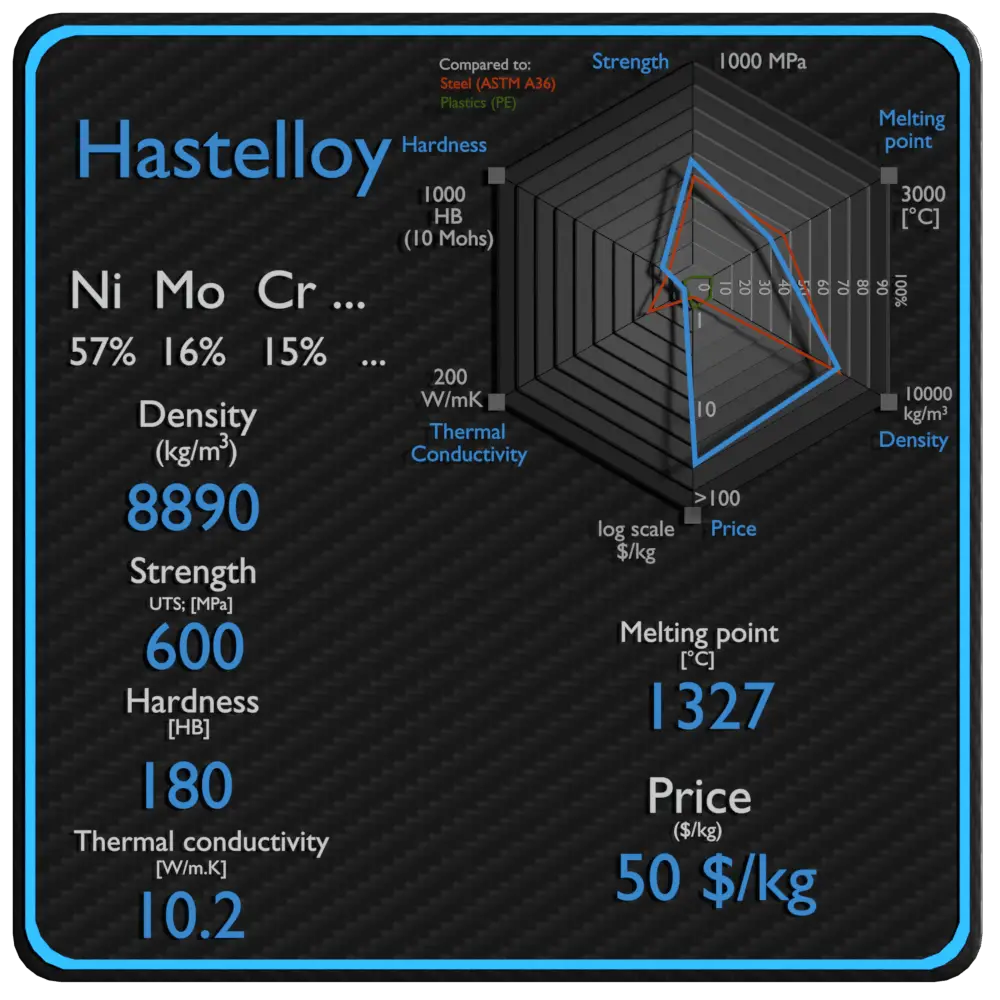
Résumé

Nom	Hastelloy
Phase à STP	solide
Densité	8890kg/m3
Résistance à la traction ultime	600 MPa
Limite d’élasticité	300 MPa
Module de Young	205 GPa
Dureté Brinell	180 BHN
Point de fusion	1327°C
Conductivité thermique	10,2 W/mK
Capacité thermique	420 J/g·K
Prix	50 $/kg

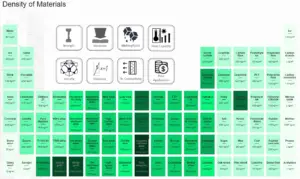
Densité d’Hastelloy

Les densités typiques de diverses substances sont à la pression atmosphérique. La densité  est définie comme la  masse par unité de volume. C’est une  propriété intensive, qui est définie mathématiquement comme la masse divisée par le volume: ρ = m/V

En d’autres termes, la densité (ρ) d’une substance est la masse totale (m) de cette substance divisée par le volume total (V) occupé par cette substance. L’unité SI standard est le kilogramme par mètre cube (kg/m³). L’unité anglaise standard est la masse de livres par pied cube (lbm/ft³).

La densité de l’Hastelloy est de 8890 kg/m³.

Exemple: Densité

Calculer la hauteur d’un cube en Hastelloy, qui pèse une tonne métrique.

Solution:

La densité est définie comme la masse par unité de volume. Il est mathématiquement défini comme la masse divisée par le volume: ρ = m/V

Comme le volume d’un cube est la troisième puissance de ses côtés (V = a³), la hauteur de ce cube peut être calculée:

La hauteur de ce cube est alors a = 0,483 m.

Propriétés mécaniques de l’Hastelloy

La force de l’Hastelloy

En mécanique des matériaux, la résistance d’un matériau est sa capacité à supporter une charge appliquée sans rupture ni déformation plastique. La résistance des matériaux considère essentiellement la relation entre les charges externes appliquées à un matériau et la déformation ou la modification des dimensions du matériau qui en résulte. Lors de la conception de structures et de machines, il est important de tenir compte de ces facteurs, afin que le matériau sélectionné ait une résistance suffisante pour résister aux charges ou forces appliquées et conserver sa forme d’origine.

La résistance d’un matériau est sa capacité à supporter cette charge appliquée sans défaillance ni déformation plastique. Pour la contrainte de traction, la capacité d’un matériau ou d’une structure à supporter des charges tendant à s’allonger est appelée résistance ultime à la traction (UTS). La limite d’élasticité ou la limite d’élasticité est la propriété du matériau définie comme la contrainte à laquelle un matériau commence à se déformer plastiquement, tandis que la limite d’élasticité est le point où la déformation non linéaire (élastique + plastique) commence. En cas de contrainte de traction d’une barre uniforme (courbe contrainte-déformation), la  loi de Hooke décrit le comportement d’une barre dans la région élastique. Le module de Young est le module d’élasticité pour la contrainte de traction et de compression dans le régime d’élasticité linéaire d’une déformation uniaxiale et est généralement évaluée par des essais de traction.

Voir aussi: Résistance des matériaux

Résistance à la traction ultime de l’Hastelloy

La résistance à la traction ultime de l’Hastelloy est de 600 MPa.

Limite d’élasticité de l’Hastelloy

La limite d’élasticité de l’Hastelloy  est de 300 MPa.

Module de Young de l’Hastelloy

Le module  de Young de l’Hastelloy est de 205 GPa.

Dureté de l’Hastelloy

En science des matériaux, la dureté est la capacité à résister à  l’indentation de surface (déformation plastique localisée) et  aux rayures. Le test de dureté Brinell est l’un des tests de dureté par indentation, qui a été développé pour les tests de dureté. Dans les tests Brinell, un pénétrateur sphérique dur est forcé sous une charge spécifique dans la surface du métal à tester.

L’  indice de dureté Brinell (HB) est la charge divisée par la surface de l’indentation. Le diamètre de l’empreinte est mesuré avec un microscope à échelle superposée. Le nombre de dureté Brinell est calculé à partir de l’équation:

La dureté Brinell de l’Hastelloy est d’environ 180 BHN (converti).

Voir aussi: Dureté des matériaux

Exemple: Force

Supposons une tige en plastique, qui est en Hastelloy. Cette tige en plastique a une section transversale de 1 cm². Calculez la force de traction nécessaire pour atteindre la résistance ultime à la traction de ce matériau, soit: UTS = 600 MPa.

Solution:

La contrainte (σ)  peut être assimilée à la charge par unité de surface ou à la force (F) appliquée par section transversale (A) perpendiculaire à la force comme suit:

par conséquent, la force de traction nécessaire pour atteindre la résistance à la traction ultime est:

F = UTS x A = 600 x 10⁶ x 0,0001 = 60 000 N

Propriétés thermiques de l’Hastelloy

Hastelloy – Point de fusion

Le point de fusion de l’Hastelloy est de 1327 °C.

Notez que ces points sont associés à la pression atmosphérique standard. En général, la fusion est un changement de phase d’une substance de la phase solide à la phase liquide. Le point de fusion d’une substance est la température à laquelle ce changement de phase se produit. Le point de fusion définit également une condition dans laquelle le solide et le liquide peuvent exister en équilibre. Pour divers composés chimiques et alliages, il est difficile de définir le point de fusion, car il s’agit généralement d’un mélange de divers éléments chimiques.

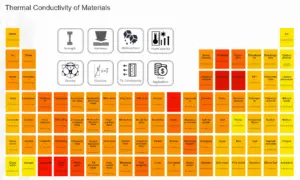
Hastelloy – Conductivité thermique

La conductivité thermique de l’Hastelloy est de 10,2 W/(m·K).

Les caractéristiques de transfert de chaleur d’un matériau solide sont mesurées par une propriété appelée la conductivité thermique, k (ou λ), mesurée en  W/mK. C’est une mesure de la capacité d’une substance à transférer de la chaleur à travers un matériau par  conduction. Notez que  la loi de Fourier s’applique à toute matière, quel que soit son état (solide, liquide ou gazeux), par conséquent, elle est également définie pour les liquides et les gaz.

La conductivité thermique de la plupart des liquides et des solides varie avec la température. Pour les vapeurs, cela dépend aussi de la pression. En général:

La plupart des matériaux sont presque homogènes, nous pouvons donc généralement écrire  k = k (T) . Des définitions similaires sont associées aux conductivités thermiques dans les directions y et z (ky, kz), mais pour un matériau isotrope, la conductivité thermique est indépendante de la direction de transfert, kx = ky = kz = k.

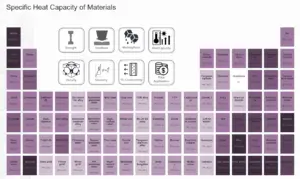
Hastelloy – Chaleur spécifique

La chaleur spécifique de l’Hastelloy est de 420 J/g K.

La chaleur spécifique, ou capacité thermique spécifique, est une propriété liée à l’énergie interne  très importante en thermodynamique. Les  propriétés intensives c_v et c_p sont définies pour des substances compressibles pures et simples comme des dérivées partielles de l’ énergie interne u(T, v) et de  l’ enthalpie h(T, p), respectivement: 

où les indices v et p désignent les variables maintenues fixes lors de la différenciation. Les propriétés c_v et c_p sont appelées chaleurs spécifiques (ou capacités calorifiques) car, dans certaines conditions particulières, elles relient le changement de température d’un système à la quantité d’énergie ajoutée par transfert de chaleur. Leurs unités SI sont J/kg K ou J/mol K.

Exemple: Calcul du transfert de chaleur

La conductivité thermique est définie comme la quantité de chaleur (en watts) transférée à travers une surface carrée de matériau d’une épaisseur donnée (en mètres) en raison d’une différence de température. Plus la conductivité thermique du matériau est faible, plus la capacité du matériau à résister au transfert de chaleur est grande.

Calculer le taux de  flux de chaleur à  travers un mur de 3 mx 10 m de surface (A = 30 m²). La paroi a une épaisseur de 15 cm (L₁) et est en Hastelloy avec une conductivité thermique de k₁ = 10,2 W/mK (mauvais isolant thermique). Supposons que les températures intérieure et extérieure  sont de 22°C et -8°C, et que les  coefficients de transfert de chaleur par convection  sur les côtés intérieur et extérieur sont h₁ = 10 W/m²K et h₂ = 30 W/m²K, respectivement. A noter que ces coefficients de convection dépendent fortement notamment des conditions ambiantes et intérieures (vent, humidité, etc.).

Calculez le flux de chaleur (perte de chaleur) à travers ce mur.

Solution:

Comme cela a été écrit, de nombreux processus de transfert de chaleur impliquent des systèmes composites et impliquent même une combinaison de  conduction  et  de convection . Avec ces systèmes composites, il est souvent pratique de travailler avec un coefficient de transfert de chaleur global, appelé  facteur U. Le facteur U est défini par une expression analogue à  la loi de refroidissement de Newton:

Le  coefficient de transfert de chaleur global est lié à la  résistance thermique totale et dépend de la géométrie du problème.

En supposant un transfert de chaleur unidimensionnel à travers la paroi plane et sans tenir compte du rayonnement, le  coefficient de transfert de chaleur global  peut être calculé comme suit:

Le coefficient de transfert thermique global  est alors: U = 1 / (1/10 + 0,15/10,2 + 1/30) = 6,75 W/m²K

Le flux de chaleur peut alors être calculé simplement comme suit: q = 6,75 [W/m²K] x 30 [K] = 202,65 W/m²

La perte totale de chaleur à travers ce mur sera de: q_perte = q . A = 202,65 [W/m²] x 30 [m²] = 6079,47 W

Propriétés et prix des autres matériaux

table-de-matériaux-en-résolution-8k