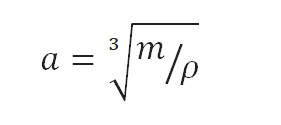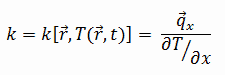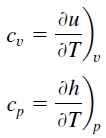Alpaca – Densidad – Resistencia – Dureza – Punto de fusión

Acerca de la Alpaca

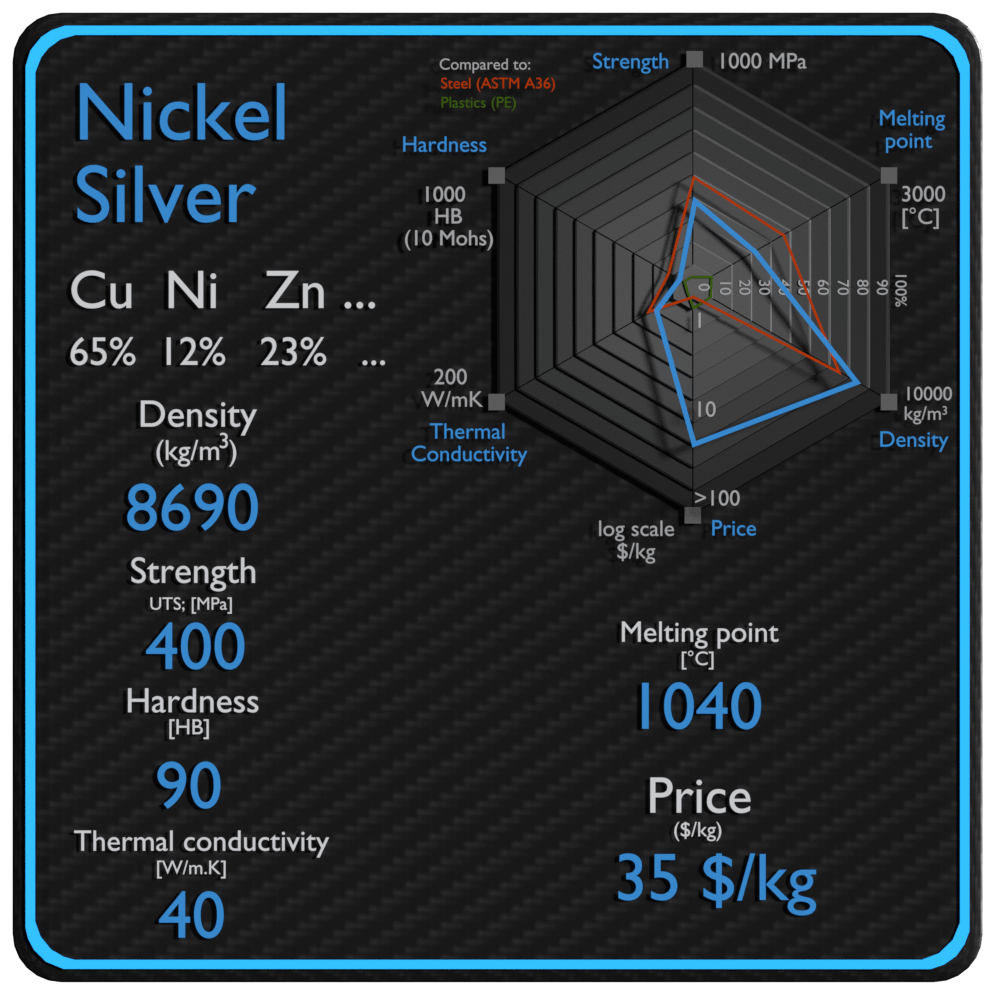
Alpaca, también conocida como plata alemana, latón de níquel o alpaca, es una aleación de cobre con níquel y, a menudo, zinc. La aleación de cobre UNS C75700 níquel plata 65-12 tiene buena resistencia a la corrosión y al deslustre, y alta conformabilidad. La alpaca recibe su nombre por su apariencia plateada, pero no contiene plata elemental a menos que esté chapada. 

Resumen

Nombre	Alpaca
Fase en STP	sólido
Densidad	8690 kg / m3
Resistencia a la tracción	400 MPa
Límite de elastacidad	170 MPa
Módulo de Young	117 GPa
Dureza Brinell	90 BHN
Punto de fusion	1040 ° C
Conductividad térmica	40 W / mK
Capacidad calorífica	377 J / g K
Precio	35 $ ​​/ kg

Densidad de la Alpaca

Las densidades típicas de varias sustancias se encuentran a presión atmosférica. La densidad  se define como la  masa por unidad de volumen . Es una  propiedad intensiva , que se define matemáticamente como masa dividida por volumen:  ρ = m / V

En palabras, la densidad (ρ) de una sustancia es la masa total (m) de esa sustancia dividida por el volumen total (V) ocupado por esa sustancia. La unidad estándar del SI es  kilogramos por metro cúbico  ( kg / m ³ ). La unidad de inglés estándar es  libras de masa por pie cúbico  ( lbm / ft ³ ).

La densidad de la Alpaca es de 8690 kg / m ³ .

Ejemplo: densidad

Calcula la altura de un cubo hecho de níquel plateado, que pesa una tonelada métrica.

Solución:

La densidad  se define como la  masa por unidad de volumen . Se define matemáticamente como masa dividida por volumen: ρ = m / V

Como el volumen de un cubo es la tercera potencia de sus lados (V = a ³ ), la altura de este cubo se puede calcular:

La altura de este cubo es entonces a = 0,486 m .

Propiedades mecánicas de la Alpaca

Resistencia de la Alpaca

En mecánica de materiales, la resistencia de un material es su capacidad para soportar una carga aplicada sin fallas ni deformaciones plásticas. La resistencia de los materiales básicamente considera la relación entre las cargas externas aplicadas a un material y la deformación resultante o cambio en las dimensiones del material. Al diseñar estructuras y máquinas, es importante considerar estos factores, a fin de que el material seleccionado tenga la resistencia adecuada para resistir las cargas o fuerzas aplicadas y conservar su forma original.

La resistencia de un material es su capacidad para soportar esta carga aplicada sin fallas ni deformaciones plásticas. Para la tensión de tracción, la capacidad de un material o estructura para soportar cargas que tienden a alargarse se conoce como resistencia máxima a la tracción (UTS). El límite elástico o límite elástico es la propiedad del material definida como el esfuerzo en el que un material comienza a deformarse plásticamente, mientras que el límite elástico es el punto donde comienza la deformación no lineal (elástica + plástica). En caso de tensión de tensión de una barra uniforme (curva tensión-deformación), la  ley de Hooke describe el comportamiento de una barra en la región elástica. El módulo de elasticidad de Young es el módulo de elasticidad para esfuerzos de tracción y compresión en el régimen de elasticidad lineal de una deformación uniaxial y generalmente se evalúa mediante ensayos de tracción.

Ver también: Resistencia de los materiales

Máxima resistencia a la tracción de la Alpaca

La resistencia máxima a la tracción de la Alpaca es de 400 MPa.

Límite de elastacidad de la Alpaca

El límite elástico de la Alpaca  es de 170 MPa.

Módulo de Young de la Alpaca

El módulo de elasticidad de Young de la Alpaca es de 117 GPa.

Dureza de la Alpaca

En la ciencia de los materiales, la  dureza  es la capacidad de resistir  la hendidura de la superficie  ( deformación plástica localizada ) y el  rayado . La prueba de dureza Brinell  es una de las pruebas de dureza por indentación, que se ha desarrollado para las pruebas de dureza. En las pruebas Brinell, se fuerza un penetrador esférico duro  bajo una carga específica en la superficie del metal que se va a probar.

El  número de dureza Brinell  (HB) es la carga dividida por el área de la superficie de la muesca. El diámetro de la impresión se mide con un microscopio con una escala superpuesta. El número de dureza Brinell se calcula a partir de la ecuación:

La dureza Brinell de la Alpaca es de aproximadamente 90 BHN (convertida).

Ver también: dureza de materiales

Ejemplo: resistencia

Suponga una varilla de plástico, que está hecha de alpaca. Esta varilla de plástico tiene un área de sección transversal de 1 cm ² . Calcule la fuerza de tracción necesaria para lograr la máxima resistencia a la tracción de este material, que es: UTS = 400 MPa.

Solución:

La tensión (σ)  se puede equiparar a la carga por unidad de área o la fuerza (F) aplicada por área de sección transversal (A) perpendicular a la fuerza como:

por lo tanto, la fuerza de tracción necesaria para lograr la máxima resistencia a la tracción es:

F = UTS x A = 400 x 10 ⁶ x 0,0001 = 40000 N

Propiedades térmicas de la Alpaca

Alpaca – Punto de fusión

Punto de Alpacal de fusión es de 1040 ° C .

Tenga en cuenta que estos puntos están asociados con la presión atmosférica estándar. En general, la  fusión  es un  cambio  de fase de una sustancia de la fase sólida a la líquida. El  punto  de fusión de una sustancia es la temperatura a la que se produce este cambio de fase. El  punto de fusión  también define una condición en la que el sólido y el líquido pueden existir en equilibrio. Para varios compuestos químicos y aleaciones, es difícil definir el punto de fusión, ya que generalmente son una mezcla de varios elementos químicos.

Alpaca – Conductividad térmica

La conductividad térmica de la Alpaca es de 40 W / (m · K) .

Las características de transferencia de calor de un material sólido se miden mediante una propiedad llamada  conductividad térmica , k (o λ), medida en  W / mK . Es una medida de la capacidad de una sustancia para transferir calor a través de un material por  conducción . Tenga en cuenta que  la ley de Fourier se  aplica a toda la materia, independientemente de su estado (sólido, líquido o gas), por lo que también se define para líquidos y gases.

La  conductividad térmica  de la mayoría de los líquidos y sólidos varía con la temperatura. Para los vapores, también depende de la presión. En general:

La mayoría de los materiales son casi homogéneos, por lo que normalmente podemos escribir  k = k (T) . Se asocian definiciones similares con las conductividades térmicas en las direcciones y y z (ky, kz), pero para un material isótropo, la conductividad térmica es independiente de la dirección de transferencia, kx = ky = kz = k.

Alpaca – Calor específico

El calor específico de Alpaca es 377  J / g K .

El calor específico, o capacidad calorífica específica,  es una propiedad relacionada con la energía interna  que es muy importante en termodinámica. Las  propiedades intensivas  c _v  y  c _p  se definen para sustancias compresibles simples puras como derivadas parciales de la  energía interna  u (T, v)  y la  entalpía  h (T, p) , respectivamente: 

donde los subíndices  v  y  p  denotan las variables que se mantienen fijas durante la diferenciación. Las propiedades  c _v  y  c _p  se denominan  calores específicos  (o  capacidades caloríficas ) porque, en determinadas condiciones especiales, relacionan el cambio de temperatura de un sistema con la cantidad de energía añadida por la transferencia de calor. Sus unidades SI son  J / kg K  o  J / mol K .

Ejemplo: cálculo de transferencia de calor

La conductividad térmica se define como la cantidad de calor (en vatios) transferida a través de un área cuadrada de material de un espesor determinado (en metros) debido a una diferencia de temperatura. Cuanto menor sea la conductividad térmica del material, mayor será la capacidad del material para resistir la transferencia de calor.

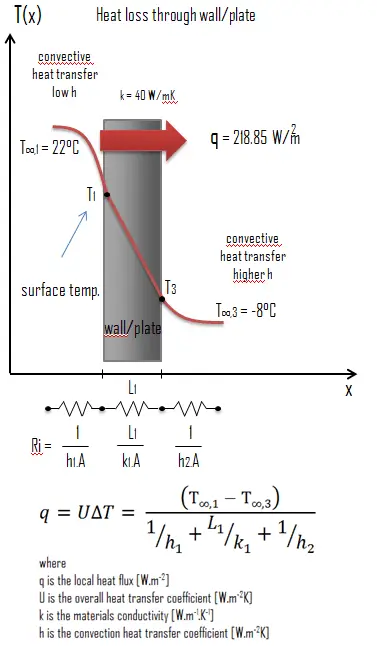
Calcule la tasa de flujo de  calor a  través de una pared de 3 mx 10 m de área (A = 30 m ² ). La pared tiene un espesor de 15 cm (L ₁ ) y está hecha de Alpaca con una conductividad térmica  de k ₁ = 40 W / mK (mal aislante térmico). Suponga que las temperaturas interior y exterior  son 22 ° C y -8 ° C, y los  coeficientes de transferencia de calor por convección  en los lados interior y exterior son h ₁  = 10 W / m ² K y h ₂  = 30 W / m ² K, respectivamente. Tenga en cuenta que estos coeficientes de convección dependen en gran medida, especialmente, de las condiciones ambientales e interiores (viento, humedad, etc.).

Calcule el flujo de calor ( pérdida de calor ) a través de esta pared.

Solución:

Como se escribió, muchos de los procesos de transferencia de calor involucran sistemas compuestos e incluso involucran una combinación de  conducción  y  convección . Con estos sistemas compuestos, a menudo es conveniente trabajar con un  coeficiente de transferencia de calor en general ,  conocido como un  factor U . El factor U se define mediante una expresión análoga a  la ley de enfriamiento de Newton :

El  coeficiente de transferencia de calor general  está relacionado con la  resistencia térmica total  y depende de la geometría del problema.

Suponiendo una transferencia de calor unidimensional a través de la pared plana y sin tener en cuenta la radiación, el  coeficiente de transferencia de calor general  se puede calcular como:

El coeficiente de transferencia de calor total  es entonces: U = 1 / (1/10 + 0,15 / 40 + 1/30) = 7,29 W / m ² K

El flujo de calor se puede calcular entonces simplemente como: q = 7,29 [W / m ² K] x 30 [K] = 218,85 W / m ²

La pérdida total de calor a través de esta pared será: q _pérdida  = q. A = 218,85 [W / m ² ] x 30 [m ² ] = 65065,35 W