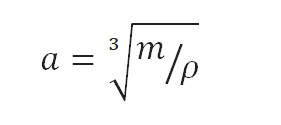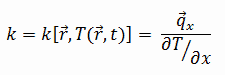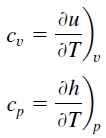Arena | Densidad, capacidad calorífica, conductividad térmica

Acerca de la arena

La arena es un material granular compuesto de roca finamente dividida y partículas minerales. La composición de la arena varía, dependiendo de las fuentes y las condiciones de las rocas locales, pero el componente más común de la arena en los entornos continentales del interior y en los entornos costeros no tropicales es la sílice (dióxido de silicio o SiO2), generalmente en forma de cuarzo. La sílice es una de las familias de materiales más complejas y abundantes, existiendo como un compuesto de varios minerales y como producto sintético.

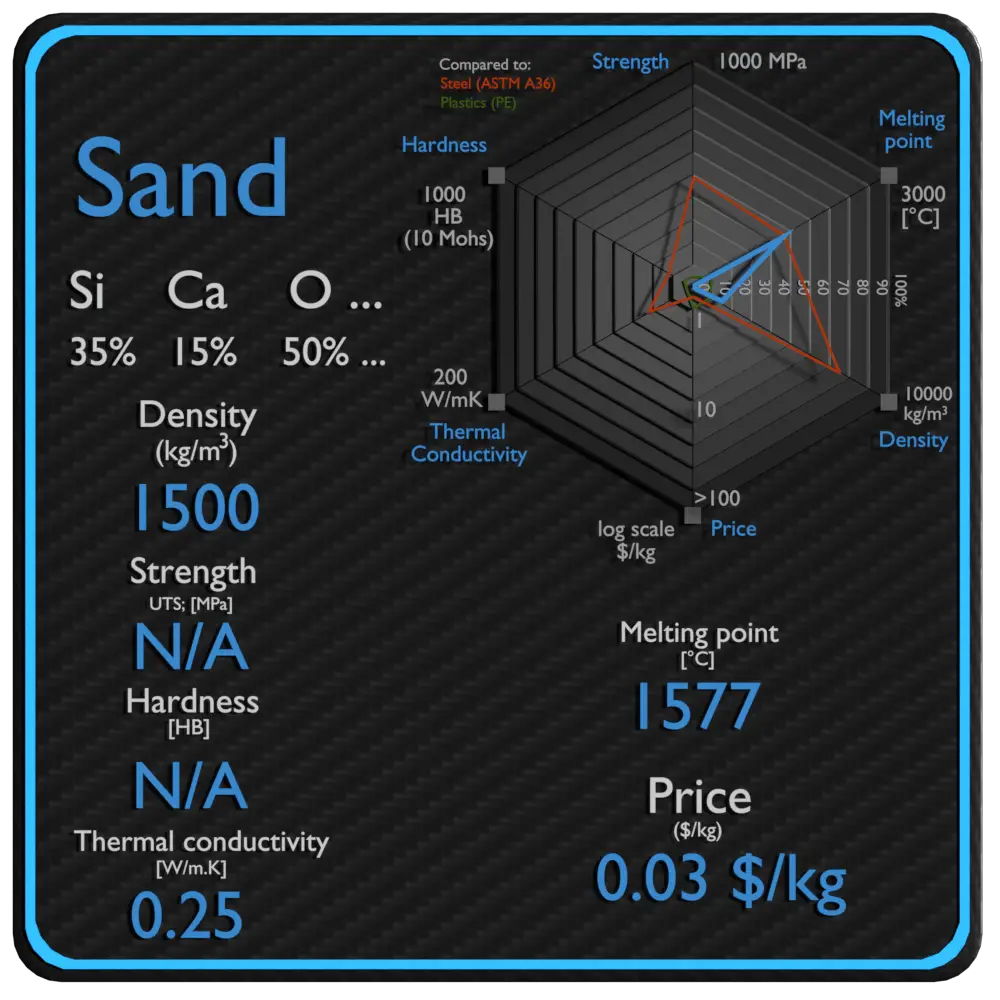
arena propiedades densidad resistencia precio

Resumen

Nombre	Arena
Fase en STP	sólido
Densidad	1500 kg / m3
Resistencia a la tracción	N / A
Límite de elastacidad	N / A
Módulo de Young	N / A
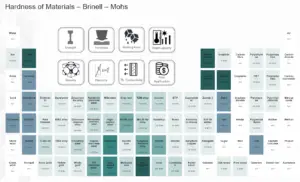
Dureza Brinell	N / A
Punto de fusion	1577 ° C
Conductividad térmica	0,25 W / mK
Capacidad calorífica	830 J / g K
Precio	0,03 $ / kg

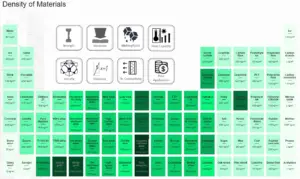
Densidad de la arena

Las densidades típicas de varias sustancias se encuentran a presión atmosférica. La densidad se define como la masa por unidad de volumen . Es una propiedad intensiva , que se define matemáticamente como masa dividida por volumen: ρ = m / V

En palabras, la densidad (ρ) de una sustancia es la masa total (m) de esa sustancia dividida por el volumen total (V) ocupado por esa sustancia. La unidad estándar del SI es kilogramos por metro cúbico ( kg / m ³ ). La unidad de inglés estándar es libras de masa por pie cúbico ( lbm / ft ³ ).

La densidad de la arena es de 1500 kg / m ³ .

Ejemplo: densidad

Calcula la altura de un cubo de arena, que pesa una tonelada métrica.

Solución:

La densidad se define como la masa por unidad de volumen . Se define matemáticamente como masa dividida por volumen: ρ = m / V

Como el volumen de un cubo es la tercera potencia de sus lados (V = a ³ ), la altura de este cubo se puede calcular:

La altura de este cubo es entonces a = 0,874 m .

Densidad de materiales

Tabla de materiales - Densidad de materiales

Propiedades térmicas de la arena

Arena – Punto de fusión

Punto de arena de fusión es de 1577 ° C .

Tenga en cuenta que estos puntos están asociados con la presión atmosférica estándar. En general, la fusión es un cambio de fase de una sustancia de la fase sólida a la líquida. El punto de fusión de una sustancia es la temperatura a la que se produce este cambio de fase. El punto de fusión también define una condición en la que el sólido y el líquido pueden existir en equilibrio. Para varios compuestos químicos y aleaciones, es difícil definir el punto de fusión, ya que generalmente son una mezcla de varios elementos químicos.

Arena – Conductividad térmica

La conductividad térmica de la arena es de 0,25 W / (m · K) .

Las características de transferencia de calor de un material sólido se miden mediante una propiedad llamada conductividad térmica , k (o λ), medida en W / mK . Es una medida de la capacidad de una sustancia para transferir calor a través de un material por conducción . Tenga en cuenta que la ley de Fourier se aplica a toda la materia, independientemente de su estado (sólido, líquido o gas), por lo tanto, también se define para líquidos y gases.

La conductividad térmica de la mayoría de los líquidos y sólidos varía con la temperatura. Para los vapores, también depende de la presión. En general:

La mayoría de los materiales son casi homogéneos, por lo que normalmente podemos escribir k = k (T) . Se asocian definiciones similares con conductividades térmicas en las direcciones y y z (ky, kz), pero para un material isótropo, la conductividad térmica es independiente de la dirección de transferencia, kx = ky = kz = k.

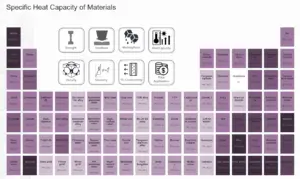
Arena – Calor específico

El calor específico de Sand es 830 J / g K .

El calor específico, o capacidad calorífica específica, es una propiedad relacionada con la energía interna que es muy importante en termodinámica. Las propiedades intensivas c _v y c _p se definen para sustancias compresibles simples puras como derivadas parciales de la energía interna u (T, v) y la entalpía h (T, p) , respectivamente:

donde los subíndices v y p denotan las variables que se mantienen fijas durante la diferenciación. Las propiedades c _v y c _p se conocen como calores específicos (o capacidades caloríficas ) porque bajo ciertas condiciones especiales relacionan el cambio de temperatura de un sistema con la cantidad de energía agregada por la transferencia de calor. Sus unidades SI son J / kg K o J / mol K .

Ejemplo: cálculo de transferencia de calor

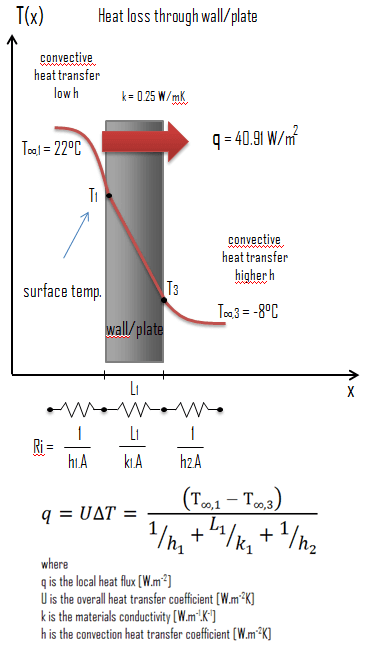La conductividad térmica se define como la cantidad de calor (en vatios) transferida a través de un área cuadrada de material de un espesor determinado (en metros) debido a una diferencia de temperatura. Cuanto menor sea la conductividad térmica del material, mayor será la capacidad del material para resistir la transferencia de calor.

Calcule la tasa de flujo de calor a través de una pared de 3 mx 10 m de área (A = 30 m ² ). La pared tiene 15 cm de espesor (L ₁ ) y está hecha de Arena con una conductividad térmica de k ₁ = 0,25 W / mK (mal aislante térmico). Suponga que las temperaturas interior y exterior son 22 ° C y -8 ° C, y los coeficientes de transferencia de calor por convección en los lados interior y exterior son h ₁ = 10 W / m ² K y h ₂ = 30 W / m ² K, respectivamente. Tenga en cuenta que estos coeficientes de convección dependen en gran medida, especialmente, de las condiciones ambientales e interiores (viento, humedad, etc.).

Calcule el flujo de calor ( pérdida de calor ) a través de esta pared.

Solución:

Como se escribió, muchos de los procesos de transferencia de calor involucran sistemas compuestos e incluso involucran una combinación de conducción y convección . Con estos sistemas compuestos, a menudo es conveniente trabajar con un coeficiente de transferencia de calor en general , conocido como un factor U . El factor U se define mediante una expresión análoga a la ley de enfriamiento de Newton :

El coeficiente de transferencia de calor general está relacionado con la resistencia térmica total y depende de la geometría del problema.

Suponiendo una transferencia de calor unidimensional a través de la pared plana y sin tener en cuenta la radiación, el coeficiente de transferencia de calor general se puede calcular como: