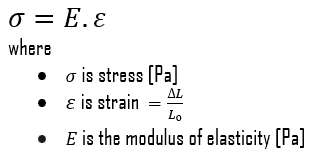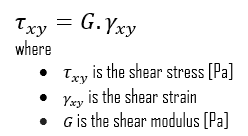À propos du Lutétium
Le lutétium est un métal blanc argenté, qui résiste à la corrosion à l’air sec, mais pas à l’air humide. Le lutétium est le dernier élément de la série des lanthanides, et il est traditionnellement compté parmi les terres rares.
Force du Lutétium
En mécanique des matériaux, la résistance d’un matériau est sa capacité à supporter une charge appliquée sans rupture ni déformation plastique. La résistance des matériaux considère essentiellement la relation entre les charges externes appliquées à un matériau et la déformation ou la modification des dimensions du matériau qui en résulte. Lors de la conception de structures et de machines, il est important de tenir compte de ces facteurs, afin que le matériau sélectionné ait une résistance suffisante pour résister aux charges ou forces appliquées et conserver sa forme d’origine. La résistance d’un matériau est sa capacité à supporter cette charge appliquée sans défaillance ni déformation plastique.
Pour la contrainte de traction, la capacité d’un matériau ou d’une structure à supporter des charges tendant à s’allonger est appelée résistance ultime à la traction (UTS). La limite d’élasticité ou la limite d’élasticité est la propriété du matériau définie comme la contrainte à laquelle un matériau commence à se déformer plastiquement, tandis que la limite d’élasticité est le point où la déformation non linéaire (élastique + plastique) commence.
Résistance à la traction ultime du Lutétium
La résistance à la traction ultime du Lutétium est N/A.
Limite d’élasticité du Lutétium
La limite d’élasticité du Lutétium est N/A.
Module de Young du Lutétium
Le module de Young du Lutétium est N/A.
Le module d’élasticité de cisaillement du lutétium est de 27,2 GPa.
Le module d’élasticité de masse du lutétium est de 47,6 GPa.
Dureté du Lutétium
En science des matériaux, la dureté est la capacité à résister à l’indentation de surface (déformation plastique localisée) et aux rayures. Le test de dureté Brinell est l’un des tests de dureté par indentation, qui a été développé pour les tests de dureté. Dans les tests Brinell, un pénétrateur sphérique dur est forcé sous une charge spécifique dans la surface du métal à tester.
La dureté Brinell du lutétium est d’environ 900 MPa.
La méthode d’essai de dureté Vickers a été développée par Robert L. Smith et George E. Sandland chez Vickers Ltd comme alternative à la méthode Brinell pour mesurer la dureté des matériaux. La méthode d’essai de dureté Vickers peut également être utilisée comme méthode d’essai de microdureté, qui est principalement utilisée pour les petites pièces, les sections minces ou les travaux en profondeur.
La dureté Vickers du lutétium est d’environ 1100 MPa.
La dureté à la rayure est la mesure de la résistance d’un échantillon à la déformation plastique permanente due au frottement d’un objet pointu. L’échelle la plus courante pour ce test qualitatif est l’échelle de Mohs, qui est utilisée en minéralogie. L’ échelle de Mohs de dureté minérale est basée sur la capacité d’un échantillon naturel de minéral à rayer visiblement un autre minéral.
Le lutétium a une dureté d’environ N/A.
Lutétium – Structure cristalline
Une structure cristalline possible du lutétium est une structure hexagonale compacte.
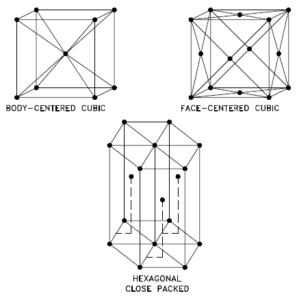
Dans les métaux et dans de nombreux autres solides, les atomes sont disposés en réseaux réguliers appelés cristaux. Un réseau cristallin est un motif répétitif de points mathématiques qui s’étend dans tout l’espace. Les forces de la liaison chimique provoquent cette répétition. C’est ce motif répété qui contrôle les propriétés telles que la résistance, la ductilité, la densité, la conductivité (propriété de conduire ou de transmettre la chaleur, l’électricité, etc.) et la forme. Il existe 14 types généraux de ces modèles connus sous le nom de réseaux de Bravais.
Structure cristalline du Lutétium

Force des éléments

Élasticité des éléments

Dureté des éléments

À propos de la force
 En mécanique des matériaux, la résistance d’un matériau est sa capacité à supporter une charge appliquée sans rupture ni déformation plastique. La résistance des matériaux considère essentiellement la relation entre les charges externes appliquées à un matériau et la déformation ou la modification des dimensions du matériau qui en résulte. Lors de la conception de structures et de machines, il est important de tenir compte de ces facteurs, afin que le matériau sélectionné ait une résistance suffisante pour résister aux charges ou forces appliquées et conserver sa forme d’origine. La résistance d’un matériau est sa capacité à supporter cette charge appliquée sans défaillance ni déformation plastique.
En mécanique des matériaux, la résistance d’un matériau est sa capacité à supporter une charge appliquée sans rupture ni déformation plastique. La résistance des matériaux considère essentiellement la relation entre les charges externes appliquées à un matériau et la déformation ou la modification des dimensions du matériau qui en résulte. Lors de la conception de structures et de machines, il est important de tenir compte de ces facteurs, afin que le matériau sélectionné ait une résistance suffisante pour résister aux charges ou forces appliquées et conserver sa forme d’origine. La résistance d’un matériau est sa capacité à supporter cette charge appliquée sans défaillance ni déformation plastique.
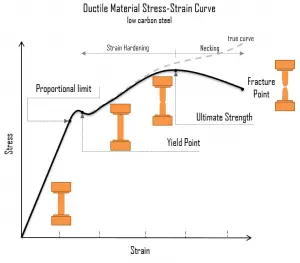
Un diagramme schématique de la courbe contrainte-déformation de l’acier à faible teneur en carbone à température ambiante est présenté dans la figure. Il existe plusieurs étapes montrant des comportements différents, ce qui suggère des propriétés mécaniques différentes. Pour clarifier, les matériaux peuvent manquer une ou plusieurs étapes indiquées sur la figure, ou avoir des étapes totalement différentes. Dans ce cas, nous devons faire la distinction entre les caractéristiques de contrainte-déformation des matériaux ductiles et fragiles. Les points suivants décrivent les différentes régions de la courbe contrainte-déformation et l’importance de plusieurs emplacements spécifiques.
- Limite proportionnelle. La limite proportionnelle correspond à l’emplacement de la contrainte à l’extrémité de la région linéaire, de sorte que le graphique contrainte-déformation est une ligne droite et le gradient sera égal au module d’élasticité du matériau. Pour les contraintes de traction et de compression, la pente de la partie de la courbe où la contrainte est proportionnelle à la déformation est appelée module de Young et la loi de Hooke s’applique. Entre la limite proportionnelle et la limite d’élasticité, la loi de Hooke devient discutable et la déformation augmente plus rapidement.
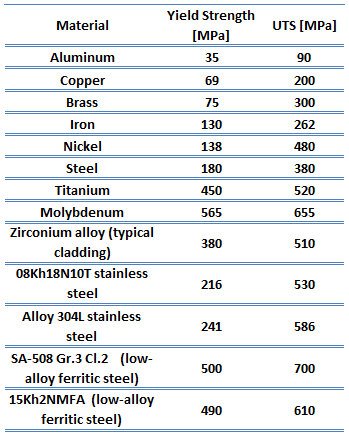 Point de rendement. La limite d’élasticité est le point sur une courbe contrainte-déformation qui indique la limite du comportement élastique et le début du comportement plastique. La limite d’élasticité ou la limite d’élasticité est la propriété du matériau définie comme la contrainte à laquelle un matériau commence à se déformer plastiquement, tandis que la limite d’élasticité est le point où la déformation non linéaire (élastique + plastique) commence. Avant la limite d’élasticité, le matériau se déforme élastiquement et reprend sa forme d’origine lorsque la contrainte appliquée est supprimée. Une fois la limite d’élasticité dépassée, une partie de la déformation sera permanente et irréversible. Certains aciers et autres matériaux présentent un comportement appelé phénomène de limite d’élasticité. Les limites d’élasticité varient de 35 MPa pour un aluminium à faible résistance à plus de 1400 MPa pour les aciers à très haute résistance.
Point de rendement. La limite d’élasticité est le point sur une courbe contrainte-déformation qui indique la limite du comportement élastique et le début du comportement plastique. La limite d’élasticité ou la limite d’élasticité est la propriété du matériau définie comme la contrainte à laquelle un matériau commence à se déformer plastiquement, tandis que la limite d’élasticité est le point où la déformation non linéaire (élastique + plastique) commence. Avant la limite d’élasticité, le matériau se déforme élastiquement et reprend sa forme d’origine lorsque la contrainte appliquée est supprimée. Une fois la limite d’élasticité dépassée, une partie de la déformation sera permanente et irréversible. Certains aciers et autres matériaux présentent un comportement appelé phénomène de limite d’élasticité. Les limites d’élasticité varient de 35 MPa pour un aluminium à faible résistance à plus de 1400 MPa pour les aciers à très haute résistance.- Résistance à la traction ultime. La résistance à la traction ultime est le maximum sur la courbe technique de contrainte-déformation. Cela correspond à la contrainte maximale qui peut être soutenu par une structure en tension. La résistance à la traction ultime est souvent abrégée en « résistance à la traction » ou même en « l’ultime ». Si cette contrainte est appliquée et maintenue, une fracture en résultera. Souvent, cette valeur est nettement supérieure à la limite d’élasticité (jusqu’à 50 à 60 % de plus que le rendement pour certains types de métaux). Lorsqu’un matériau ductile atteint sa résistance ultime, il subit une striction où la section transversale se réduit localement. La courbe contrainte-déformation ne contient pas de contrainte supérieure à la résistance ultime. Même si les déformations peuvent continuer à augmenter, la contrainte diminue généralement après que la résistance ultime a été atteinte. C’est une propriété intensive; sa valeur ne dépend donc pas de la taille de l’éprouvette. Cependant, cela dépend d’autres facteurs, température de l’environnement et du matériau d’essai. Les résistances ultimes à la traction varient de 50 MPa pour un aluminium jusqu’à 3000 MPa pour les aciers à très haute résistance.
- Point de rupture: Le point de rupture est le point de déformation où le matériau se sépare physiquement. À ce point, la déformation atteint sa valeur maximale et le matériau se rompt effectivement, même si la contrainte correspondante peut être inférieure à la résistance ultime à ce point. Les matériaux ductiles ont une résistance à la rupture inférieure à la résistance ultime à la traction (UTS), alors que dans les matériaux fragiles, la résistance à la rupture est équivalente à l’UTS. Si un matériau ductile atteint sa résistance ultime à la traction dans une situation de charge contrôlée, il continuera à se déformer, sans application de charge supplémentaire, jusqu’à ce qu’il se rompe. Cependant, si le chargement est contrôlé en déplacement, la déformation du matériau peut soulager la charge, empêchant la rupture.
À propos du module d'élasticité
En cas de contrainte de traction d’une barre uniforme (courbe contrainte-déformation), la loi de Hooke décrit le comportement d’une barre dans la région élastique. Dans cette région, l’allongement de la barre est directement proportionnel à la force de traction et à la longueur de la barre et inversement proportionnel à la section transversale et au module d’élasticité. Jusqu’à une contrainte limite, une caisse pourra retrouver ses dimensions au retrait de la charge. Les contraintes appliquées font que les atomes d’un cristal se déplacent de leur position d’équilibre. Tous les atomes sont déplacés de la même quantité et conservent toujours leur géométrie relative. Lorsque les contraintes sont supprimées, tous les atomes reviennent à leur position d’origine et aucune déformation permanente ne se produit. Selon la loi de Hooke, la contrainte est proportionnelle à la déformation (dans la région élastique) et la pente est le module de Young.
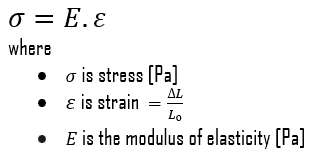 Nous pouvons étendre la même idée de relier la contrainte à la déformation aux applications de cisaillement dans la région linéaire, en reliant la contrainte de cisaillement à la déformation de cisaillement pour créer la loi de Hooke pour la contrainte de cisaillement:
Nous pouvons étendre la même idée de relier la contrainte à la déformation aux applications de cisaillement dans la région linéaire, en reliant la contrainte de cisaillement à la déformation de cisaillement pour créer la loi de Hooke pour la contrainte de cisaillement:
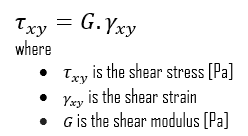
Pour les matériaux isotropes dans la région élastique, vous pouvez relier le coefficient de Poisson (ν), le module d’élasticité de Young (E) et le module d’élasticité de cisaillement (G):

Les modules élastiques propres aux matériaux polycristallins :
- Module de Young. Le module d’élasticité de Young est le module d’élasticité pour les contraintes de traction et de compression dans le régime d’élasticité linéaire d’une déformation uniaxiale et est généralement évalué par des essais de traction.
- Module d’élasticité de cisaillement. Le module de cisaillement, ou module de rigidité, est dérivé de la torsion d’une éprouvette cylindrique. Il décrit la réponse du matériau à la contrainte de cisaillement. Son symbole est G. Le module de cisaillement est l’une des nombreuses quantités permettant de mesurer la rigidité des matériaux et il apparaît dans la loi de Hooke généralisée.
- Module d’élasticité de masse. Le module d’élasticité de masse décrit l’élasticité volumétrique ou la tendance d’un objet à se déformer dans toutes les directions lorsqu’il est uniformément chargé dans toutes les directions. Par exemple, il décrit la réponse élastique à la pression hydrostatique et à la tension équilatérale (comme la pression au fond de l’océan ou d’une piscine profonde). C’est aussi la propriété d’un matériau qui détermine la réponse élastique à l’application d’une contrainte. Pour un fluide, seul le module de masse est significatif.
À propos de la dureté
En science des matériaux, la dureté est la capacité à résister à l’indentation de surface (déformation plastique localisée) et aux rayures. La dureté est probablement la propriété matérielle la plus mal définie car elle peut indiquer une résistance aux rayures, une résistance à l’abrasion, une résistance à l’indentation ou encore une résistance à la mise en forme ou à la déformation plastique localisée. La dureté est importante d’un point de vue technique car la résistance à l’usure par frottement ou érosion par la vapeur, l’huile et l’eau augmente généralement avec la dureté.
Il existe trois principaux types de mesures de dureté:
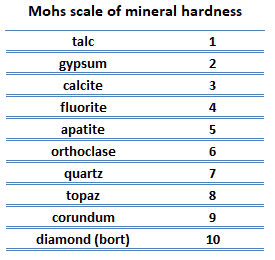 Dureté aux rayures. La dureté à la rayure est la mesure de la résistance d’un échantillon à la déformation plastique permanente due au frottement d’un objet pointu. L’échelle la plus courante pour ce test qualitatif est l’échelle de Mohs, qui est utilisée en minéralogie. L’ échelle de Mohs de dureté minérale est basée sur la capacité d’un échantillon naturel de minéral à rayer visiblement un autre minéral. La dureté d’un matériau est mesurée par rapport à l’échelle en trouvant le matériau le plus dur que le matériau donné peut rayer, ou le matériau le plus doux qui peut rayer le matériau donné. Par exemple, si un matériau est rayé par la topaze mais pas par le quartz, sa dureté sur l’échelle de Mohs se situerait entre 7 et 8.
Dureté aux rayures. La dureté à la rayure est la mesure de la résistance d’un échantillon à la déformation plastique permanente due au frottement d’un objet pointu. L’échelle la plus courante pour ce test qualitatif est l’échelle de Mohs, qui est utilisée en minéralogie. L’ échelle de Mohs de dureté minérale est basée sur la capacité d’un échantillon naturel de minéral à rayer visiblement un autre minéral. La dureté d’un matériau est mesurée par rapport à l’échelle en trouvant le matériau le plus dur que le matériau donné peut rayer, ou le matériau le plus doux qui peut rayer le matériau donné. Par exemple, si un matériau est rayé par la topaze mais pas par le quartz, sa dureté sur l’échelle de Mohs se situerait entre 7 et 8.- Dureté d’indentation. La dureté d’indentation mesure la capacité à résister à l’indentation de surface (déformation plastique localisée) et la résistance d’un échantillon à la déformation du matériau due à une charge de compression constante d’un objet pointu. Les tests de dureté par indentation sont principalement utilisés dans les domaines de l’ingénierie et de la métallurgie. Les méthodes traditionnelles sont basées sur des tests physiques de dureté par empreinte bien définis. Des pénétrateurs très durs de géométries et de tailles définies sont enfoncés en continu dans le matériau sous une force particulière. Les paramètres de déformation, tels que la profondeur d’indentation dans la méthode Rockwell, sont enregistrés pour donner des mesures de dureté. Les échelles de dureté d’indentation courantes sont Brinell, Rockwell et Vickers.
- Dureté de rebond. La dureté de rebond, également connue sous le nom de dureté dynamique, mesure la hauteur du « rebond » d’un marteau à pointe de diamant tombé d’une hauteur fixe sur un matériau. L’un des appareils utilisés pour prendre cette mesure est connu sous le nom de scléroscope. Il se compose d’une bille d’acier lâchée d’une hauteur fixe. Ce type de dureté est lié à l’élasticité.
À propos de la structure cristalline
Les trois motifs cristallins de base les plus courants sont :
- cci. Dans un arrangement d’atomes bcc (BCC), la cellule unitaire se compose de huit atomes aux coins d’un cube et d’un atome au centre du corps du cube. Dans un arrangement bcc, une cellule unitaire contient (8 atomes de coin × ⅛) + (1 atome central × 1) = 2 atomes. Le garnissage est plus efficace (68%) que le simple cubique et la structure est courante pour les métaux alcalins et les métaux de transition précoce. Les métaux contenant des structures BCC comprennent la ferrite, le chrome, le vanadium, le molybdène et le tungstène. Ces métaux possèdent une résistance élevée et une faible ductilité.
- fcc. Dans un arrangement d’atomes fcc (FCC), la cellule unitaire se compose de huit atomes aux coins d’un cube et d’un atome au centre de chacune des faces du cube. Dans un arrangement fcc, une cellule unitaire contient (8 atomes de coin × ⅛) + (6 atomes de face × ½) = 4 atomes. Cette structure, avec son parent hexagonal (hcp), a le garnissage le plus efficace (74%). Les métaux contenant des structures FCC comprennent l’austénite, l’aluminium, le cuivre, le plomb, l’argent, l’or, le nickel, le platine et le thorium. Ces métaux possèdent une faible résistance et une ductilité élevée.
- hcp. Dans un arrangement d’atomes hcp (HCP), la cellule unitaire est constituée de trois couches d’atomes. Les couches supérieure et inférieure contiennent six atomes aux coins d’un hexagone et un atome au centre de chaque hexagone. La couche intermédiaire contient trois atomes nichés entre les atomes des couches supérieure et inférieure, d’où le nom de compact. Hexagonal Close Packed (hcp) est l’un des deux types simples de garnissage atomique avec la densité la plus élevée, l’autre étant le cubique à faces centrées (fcc). Cependant, contrairement au fcc, ce n’est pas un réseau de Bravais car il existe deux ensembles non équivalents de points de réseau. Les métaux contenant des structures HCP comprennent le béryllium, le magnésium, le zinc, le cadmium, le cobalt, le thallium et le zirconium. Les métaux HCP ne sont pas aussi ductiles que les métaux FCC.
Résumé
| Élément |
Lutétium |
| Résistance à la traction ultime |
N / A |
| Limite d’élasticité |
N / A |
| Module de Young |
68,6 GPa |
| Module d’élasticité de cisaillement |
27,2 GPa |
| Module d’élasticité de masse |
47,6 GPa |
| Échelle de Mohs |
N / A |
| Dureté Brinell |
900 MPa |
| Dureté Vickers |
1100 MPa |

Source : www.luciteria.com
Propriétés des autres éléments
Autres propriétés du Lutétium