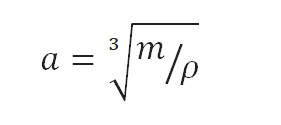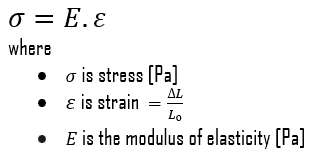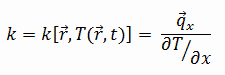Ferro Fundido Dúctil – Densidade – Resistência – Dureza – Ponto de Fusão

Sobre Ferro Fundido Dúctil

O ferro dúctil, também conhecido como ferro nodular ou ferro grafite esferoidal, é muito semelhante ao ferro cinzento em composição, mas durante a solidificação o grafite nuclea como partículas esféricas (nódulos) em ferro dúctil, em vez de flocos. O ferro dúctil não é um material único, mas parte de um grupo de materiais que podem ser produzidos com uma ampla gama de propriedades através do controle de sua microestrutura. A fase da matriz que envolve essas partículas é perlita ou ferrita, dependendo do tratamento térmico. O ferro dúctil é mais forte e mais resistente ao choque do que o ferro cinzento, portanto, embora seja mais caro devido aos ligantes, pode ser a escolha econômica preferida porque uma fundição mais leve pode desempenhar a mesma função.

Resumo

Nome	Ferro Fundido Dúctil
Fase em STP	sólido
Densidade	7300 kg/m3
Resistência à tração	414 MPa
Força de rendimento	276 MPa
Módulo de elasticidade de Young	170 GPa
Dureza Brinell	180 BHN
Ponto de fusão	1150 °C
Condutividade térmica	36 W/mK
Capacidade de calor	460 J/gK
Preço	3 $/kg

Densidade do Ferro Fundido Dúctil

As densidades típicas de várias substâncias estão à pressão atmosférica. A densidade é definida como a massa por unidade de volume. É uma propriedade intensiva, que é matematicamente definida como massa dividida pelo volume: ρ = m/V.

Em palavras, a densidade (ρ) de uma substância é a massa total (m) dessa substância dividida pelo volume total (V) ocupado por essa substância. A unidade padrão do SI é quilogramas por metro cúbico (kg/m³). A unidade padrão inglesa é libras de massa por pé cúbico (lbm/ft³).

A densidade do ferro fundido dúctil é de 7300 kg/m³.

Exemplo: Densidade

Calcule a altura de um cubo feito de ferro fundido dúctil, que pesa uma tonelada métrica.

Solução:

A densidade é definida como a massa por unidade de volume. É matematicamente definido como massa dividida pelo volume: ρ = m/V.

Como o volume de um cubo é a terceira potência de seus lados (V = a³), a altura desse cubo pode ser calculada:

A altura deste cubo é então a = 0,515 m.

Propriedades Mecânicas do Ferro Fundido Dúctil

Os materiais são frequentemente escolhidos para várias aplicações porque possuem combinações desejáveis ​​de características mecânicas. Para aplicações estruturais, as propriedades do material são cruciais e os engenheiros devem levá-las em consideração.

Resistência do Ferro Fundido Dúctil – ASTM A536 – 60-40-18

Na mecânica dos materiais, a resistência de um material é sua capacidade de suportar uma carga aplicada sem falha ou deformação plástica. A resistência dos materiais considera basicamente a relação entre as cargas externas aplicadas a um material e a deformação resultante ou alteração nas dimensões do material. A resistência de um material é sua capacidade de suportar esta carga aplicada sem falha ou deformação plástica.

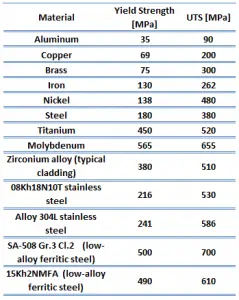
Resistência à tração

A resistência máxima à tração do Ferro Fundido Dúctil – ASTM A536 – 60-40-18 é 414 MPa (>60 ksi).

A resistência à tração final é o máximo na curva tensão-deformação de engenharia. Isso corresponde à tensão máxima que pode ser sustentado por uma estrutura em tensão. A resistência à tração final é muitas vezes encurtada para “resistência à tração” ou mesmo para “o máximo”. Se esse estresse for aplicado e mantido, resultará em fratura. Muitas vezes, esse valor é significativamente maior do que a tensão de escoamento (até 50 a 60 por cento a mais do que o escoamento para alguns tipos de metais). Quando um material dúctil atinge sua resistência máxima, ele sofre um estreitamento onde a área da seção transversal se reduz localmente. A curva tensão-deformação não contém tensão superior à resistência última. Mesmo que as deformações possam continuar a aumentar, a tensão geralmente diminui depois que a resistência máxima é alcançada. É uma propriedade intensiva; portanto, seu valor não depende do tamanho do corpo de prova. No entanto, depende de outros fatores, como a preparação do corpo de prova, temperatura do ambiente de teste e do material. A resistência à tração final varia de 50 MPa para um alumínio até 3000 MPa para aços de alta resistência.

Força de rendimento

O limite de escoamento do Ferro Fundido Dúctil – ASTM A536 – 60-40-18 é 276 MPa (>40 ksi).

O limite de escoamento é o ponto em uma curva tensão-deformação que indica o limite do comportamento elástico e o comportamento plástico inicial. Força de rendimento ou tensão de escoamento é a propriedade do material definida como a tensão na qual um material começa a se deformar plasticamente, enquanto o limite de escoamento é o ponto onde a deformação não linear (elástica + plástica) começa. Antes do limite de escoamento, o material se deformará elasticamente e retornará à sua forma original quando a tensão aplicada for removida. Uma vez ultrapassado o limite de escoamento, alguma fração da deformação será permanente e irreversível. Alguns aços e outros materiais apresentam um comportamento denominado fenômeno de limite de escoamento. Os limites de escoamento variam de 35 MPa para um alumínio de baixa resistência a mais de 1400 MPa para aços de alta resistência.

Módulo de elasticidade de Young

O módulo de elasticidade de Young Ferro Fundido Dúctil – ASTM A536 – 60-40-18 é 170 GPa.

O módulo de elasticidade de Young é o módulo de elasticidade para tensões de tração e compressão no regime de elasticidade linear de uma deformação uniaxial e geralmente é avaliado por ensaios de tração. Até uma tensão limitante, um corpo poderá recuperar suas dimensões na remoção da carga. As tensões aplicadas fazem com que os átomos em um cristal se movam de sua posição de equilíbrio. Todos os átomos são deslocados na mesma quantidade e ainda mantêm sua geometria relativa. Quando as tensões são removidas, todos os átomos retornam às suas posições originais e nenhuma deformação permanente ocorre. De acordo com a lei de Hooke, a tensão é proporcional à deformação (na região elástica), e a inclinação é o módulo de Young. O módulo de Young é igual à tensão longitudinal dividida pela deformação.

Dureza do Ferro Fundido Dúctil – ASTM A536 – 60-40-18

A dureza Brinell do Ferro Fundido Dúctil – ASTM A536 – 60-40-18 é de aproximadamente 150 – 180 MPa.

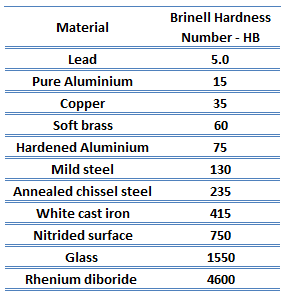Na ciência dos materiais, a dureza é a capacidade de suportar o recuo da superfície (deformação plástica localizada) e arranhões. A dureza é provavelmente a propriedade do material mais mal definida, pois pode indicar resistência a arranhões, resistência à abrasão, resistência à indentação ou mesmo resistência à conformação ou deformação plástica localizada. A dureza é importante do ponto de vista da engenharia porque a resistência ao desgaste por fricção ou erosão por vapor, óleo e água geralmente aumenta com a dureza.

O teste de dureza Brinell é um dos testes de dureza de indentação, que foi desenvolvido para testes de dureza. Nos testes Brinell, um penetrador esférico duro é forçado sob uma carga específica na superfície do metal a ser testado. O teste típico usa uma esfera de aço endurecido de 10 mm (0,39 pol) de diâmetro  como um penetrador com uma força de 3.000 kgf (29,42 kN; 6.614 lbf). A carga é mantida constante por um tempo especificado (entre 10 e 30 s). Para materiais mais macios, uma força menor é usada; para materiais mais duros, uma esfera de carboneto de tungstênio é substituída pela esfera de aço.

O teste fornece resultados numéricos para quantificar a dureza de um material, que é expressa pelo número de dureza Brinell – HB. O número de dureza Brinell é designado pelos padrões de teste mais comumente usados ​​(ASTM E10-14[2] e ISO 6506–1:2005) como HBW (H de dureza, B de brinell e W do material do penetrador, tungstênio (volfrâmio) carboneto). Nos padrões anteriores, HB ou HBS eram usados ​​para se referir a medições feitas com penetradores de aço.

O número de dureza Brinell (HB) é a carga dividida pela área da superfície da indentação. O diâmetro da impressão é medido com um microscópio com uma escala sobreposta. O número de dureza Brinell é calculado a partir da equação:

Há uma variedade de métodos de teste de uso comum (por exemplo, Brinell, Knoop , Vickers e Rockwell). Existem tabelas disponíveis correlacionando os números de dureza dos diferentes métodos de teste onde a correlação é aplicável. Em todas as escalas, um número de dureza alto representa um metal duro.

Exemplo: Força

Suponha uma haste de plástico, que é feita de ferro fundido dúctil. Esta haste de plástico tem uma área de seção transversal de 1 cm². Calcule a força de tração necessária para atingir a resistência à tração final para este material, que é: UTS = 414 MPa.

Solução:

A tensão (σ) pode ser igualada à carga por unidade de área ou à força (F) aplicada por área de seção transversal (A) perpendicular à força como:

portanto, a força de tração necessária para atingir a resistência à tração final é:

F = UTS x A = 414 x 10⁶ x 0,0001 = 41400 N

Propriedades Térmicas do Ferro Fundido Dúctil

As propriedades térmicas dos materiais referem-se à resposta dos materiais às mudanças em sua thermodynamics/thermodynamic-properties/what-is-temperature-physics/”>temperatura e à aplicação de calor. À medida que um sólido absorve thermodynamics/what-is-energy-physics/”>energia na forma de calor, sua temperatura aumenta e suas dimensões aumentam. Mas materiais diferentes reagem à aplicação de calor de forma diferente.

Capacidade de calor, expansão térmica e condutividade térmica são propriedades que são frequentemente críticas no uso prático de sólidos.

Ponto de fusão do Ferro Fundido Dúctil – ASTM A536 – 60-40-18

O ponto de fusão do Ferro Fundido Dúctil – ASTM A536 – aço 60-40-18 é em torno de 1150 °C.

Em geral, a fusão é uma mudança de fase de uma substância da fase sólida para a líquida. O ponto de fusão de uma substância é a temperatura na qual essa mudança de fase ocorre. O ponto de fusão também define uma condição na qual o sólido e o líquido podem existir em equilíbrio.

Condutividade Térmica de Ferro Fundido Dúctil – ASTM A536 – 60-40-18

A condutividade térmica do ferro fundido dúctil é 36 W/(mK).

As características de transferência de calor de um material sólido são medidas por uma propriedade chamada condutividade térmica, k (ou λ), medida em W/mK. É uma medida da capacidade de uma substância de transferir calor através de um material por condução. Observe que a lei de Fourier se aplica a toda matéria, independentemente de seu estado (sólido, líquido ou gasoso), portanto, também é definida para líquidos e gases.

A condutividade térmica da maioria dos líquidos e sólidos varia com a temperatura. Para vapores, também depende da pressão. No geral:

A maioria dos materiais são quase homogêneos, portanto, geralmente podemos escrever k = k(T). Definições semelhantes estão associadas a condutividades térmicas nas direções y e z (ky, kz), mas para um material isotrópico a condutividade térmica é independente da direção de transferência, kx = ky = kz = k.

Exemplo: cálculo de transferência de calor

A condutividade térmica é definida como a quantidade de calor (em watts) transferida através de uma área quadrada de material de determinada espessura (em metros) devido a uma diferença de temperatura. Quanto menor a condutividade térmica do material, maior a capacidade do material de resistir à transferência de calor.

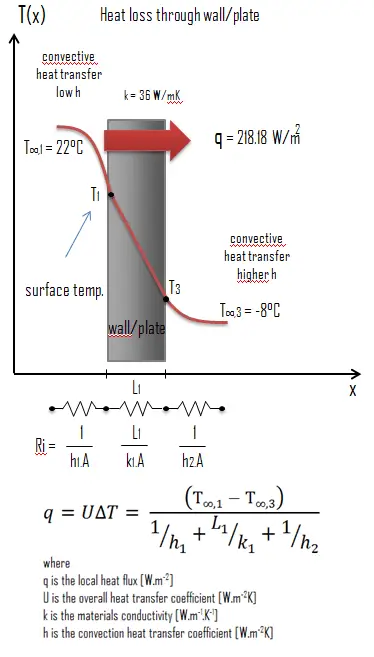
Calcule a taxa de fluxo de calor através de uma parede de 3 m x 10 m de área (A = 30 m²). A parede tem 15 cm de espessura (L₁) e é feita de Ferro Fundido Dúctil com condutividade térmica de k₁ = 36 W/mK (isolante térmico ruim). Suponha que as temperaturas interna e externa  sejam 22 °C e -8 °C, e os  coeficientes de transferência de calor por convecção nos lados interno e externo sejam h₁ = 10 W/m²K e h₂ = 30 W/m²K, respectivamente. Note-se que estes coeficientes de convecção dependem muito especialmente das condições ambientais e interiores (vento, humidade, etc.).

Calcule o fluxo de calor (perda de calor) através desta parede.

Solução:

Como foi escrito, muitos dos processos de transferência de calor envolvem sistemas compostos e até envolvem uma combinação de condução e convecção. Com esses sistemas compostos, muitas vezes é conveniente trabalhar com um coeficiente global de transferência de calor, conhecido como fator U. O fator U é definido por uma expressão análoga à lei de resfriamento de Newton:

O coeficiente global de transferência de calor está relacionado com a resistência térmica total e depende da geometria do problema.

Assumindo a transferência de calor unidimensional através da parede plana e desconsiderando a radiação, o coeficiente global de transferência de calor pode ser calculado como:

O coeficiente global de transferência de calor é então: U = 1 / (1/10 + 0,15/36 + 1/30) = 7,27 W/m²K

O fluxo de calor pode então ser calculado simplesmente como: q = 7,27 [W/m²K] x 30 [K] = 218,18 W/m²

A perda total de calor através desta parede será: q_perda = q . A = 218,18 [W/m²] x 30 [m²] = 6545,46 W