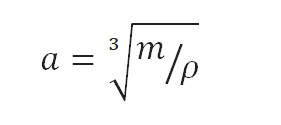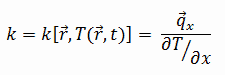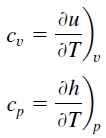Liga TZM – Densidade – Resistência – Dureza – Ponto de Fusão

Sobre a Liga TZM

As ligas de molibdênio-titânio-zircônio (TZM) contêm pequenas quantidades de titânio e zircônio dopadas com pequenas quantidades de carbonetos muito finos. Esta liga pertence às ligas refratárias, que são bem conhecidas por sua extraordinária resistência ao calor e ao desgaste. O principal requisito para suportar altas temperaturas é um alto ponto de fusão e propriedades mecânicas estáveis ​​(por exemplo, alta dureza) mesmo em altas temperaturas. Esta liga funciona de forma mais eficiente em faixas de temperatura de 700-1400 °C. A liga apresenta maior resistência à fluência e resistência a altas temperaturas, possibilitando temperaturas de serviço acima de 1060 °C para o material. É tipicamente fabricado por processos de metalurgia do pó ou fundição a arco.

Densidade da liga TZM

As densidades típicas de várias substâncias estão à pressão atmosférica. A densidade é definida como a massa por unidade de volume. É uma propriedade intensiva, que é matematicamente definida como massa dividida pelo volume: ρ = m/V.

Em palavras, a densidade (ρ) de uma substância é a massa total (m) dessa substância dividida pelo volume total (V) ocupado por essa substância. A unidade padrão do SI é quilogramas por metro cúbico (kg/m³). A unidade padrão inglesa é libras de massa por pé cúbico (lbm/ft³).

A densidade da liga TZM é 10220 kg/m³.

Exemplo: Densidade

Calcule a altura de um cubo feito de liga TZM, que pesa uma tonelada métrica.

Solução:

A densidade é definida como a massa por unidade de volume. É matematicamente definido como massa dividida pelo volume: ρ = m/V.

Como o volume de um cubo é a terceira potência de seus lados (V = a³), a altura desse cubo pode ser calculada:

A altura desse cubo é então a = 0,461 m.

Propriedades Mecânicas da Liga TZM

Força da Liga TZM

Na mecânica dos materiais, a resistência de um material é sua capacidade de suportar uma carga aplicada sem falha ou deformação plástica. A resistência dos materiais considera basicamente a relação entre as cargas externas aplicadas a um material e a deformação resultante ou alteração nas dimensões do material. Ao projetar estruturas e máquinas, é importante considerar esses fatores, para que o material selecionado tenha resistência adequada para resistir às cargas ou forças aplicadas e manter sua forma original.

A resistência de um material é sua capacidade de suportar esta carga aplicada sem falha ou deformação plástica. Para tensão de tração, a capacidade de um material ou estrutura de suportar cargas que tendem a se alongar é conhecida como resistência à tração final (UTS). O limite de escoamento ou tensão de escoamento é a propriedade do material definida como a tensão na qual um material começa a se deformar plasticamente, enquanto o ponto de escoamento é o ponto onde a deformação não linear (elástica + plástica) começa. No caso de tensão tracional de uma barra uniforme (curva tensão-deformação), a lei de Hooke descreve o comportamento de uma barra na região elástica. O módulo de elasticidade de Young é o módulo de elasticidade para tensões de tração e compressão no regime de elasticidade linear de uma deformação uniaxial e geralmente é avaliado por ensaios de tração.

Veja também: Resistência dos Materiais

Resistência à tração final da Liga TZM

A resistência à tração final da Liga TZM é de 800 MPa.

Força de Cedência da Liga TZM

O limite de escoamento da Liga TZM é N/A.

Módulo de Elasticidade da Liga TZM

O módulo de elasticidade de Young da Liga TZM é de 320 GPa.

Dureza da Liga TZM

Na ciência dos materiais, a dureza é a capacidade de suportar o recuo da superfície (deformação plástica localizada) e arranhões. O teste de dureza Brinell é um dos testes de dureza de indentação, que foi desenvolvido para testes de dureza. Nos testes Brinell, um penetrador esférico duro é forçado sob uma carga específica na superfície do metal a ser testado.

O número de dureza Brinell (HB) é a carga dividida pela área da superfície da indentação. O diâmetro da impressão é medido com um microscópio com uma escala sobreposta. O número de dureza Brinell é calculado a partir da equação:

A dureza Brinell da Liga TZM é de aproximadamente 220 BHN (convertida).

Veja também: Dureza dos Materiais

Exemplo: Força

Suponha uma haste de plástico, que é feita de liga TZM. Esta haste de plástico tem uma área de seção transversal de 1 cm². Calcule a força de tração necessária para atingir a resistência à tração final para este material, que é: UTS = 800 MPa.

Solução:

A tensão (σ) pode ser igualada à carga por unidade de área ou à força (F) aplicada por área de seção transversal (A) perpendicular à força como:

portanto, a força de tração necessária para atingir a resistência à tração final é:

F = UTS x A = 800 x 10⁶ x 0,0001 = 80000 N

Propriedades Térmicas da Liga TZM

Liga TZM – Ponto de Fusão

O ponto de fusão da Liga TZM é 2597 °C.

Observe que esses pontos estão associados à pressão atmosférica padrão. Em geral, a fusão é uma mudança de fase de uma substância da fase sólida para a líquida. O ponto de fusão de uma substância é a temperatura na qual essa mudança de fase ocorre. O ponto de fusão também define uma condição na qual o sólido e o líquido podem existir em equilíbrio. Para vários compostos químicos e ligas, é difícil definir o ponto de fusão, pois geralmente são uma mistura de vários elementos químicos.

Liga TZM – Condutividade Térmica

A condutividade térmica da Liga TZM é de 126 W/(m·K).

As características de transferência de calor de um material sólido são medidas por uma propriedade chamada condutividade térmica, k (ou λ), medida em W/mK. É uma medida da capacidade de uma substância de transferir calor através de um material por condução. Observe que a lei de Fourier se aplica a toda matéria, independentemente de seu estado (sólido, líquido ou gasoso), portanto, também é definida para líquidos e gases.

A condutividade térmica da maioria dos líquidos e sólidos varia com a temperatura. Para vapores, também depende da pressão. No geral:

A maioria dos materiais são quase homogêneos, portanto, geralmente podemos escrever k = k (T). Definições semelhantes estão associadas a condutividades térmicas nas direções y e z (ky, kz), mas para um material isotrópico a condutividade térmica é independente da direção de transferência, kx = ky = kz = k.

Liga TZM – Calor Específico

O calor específico da Liga TZM é 305 J/gK.

Calor específico, ou capacidade calorífica específica, é uma propriedade relacionada à energia interna que é muito importante na termodinâmica. As propriedades intensivas c_v e c_p são definidas para substâncias compressíveis puras simples como derivadas parciais da energia interna u(T, v) e entalpia h(T, p), respectivamente: 

onde os subscritos v e p denotam as variáveis ​​mantidas fixas durante a diferenciação. As propriedades c_v e c_p são chamadas de calores específicos (ou capacidades térmicas) porque, sob certas condições especiais, elas relacionam a mudança de temperatura de um sistema com a quantidade de energia adicionada pela transferência de calor. Suas unidades no SI são J/kg K ou J/mol K.

Exemplo: cálculo de transferência de calor

A condutividade térmica é definida como a quantidade de calor (em watts) transferida através de uma área quadrada de material de determinada espessura (em metros) devido a uma diferença de temperatura. Quanto menor a condutividade térmica do material, maior a capacidade do material de resistir à transferência de calor.

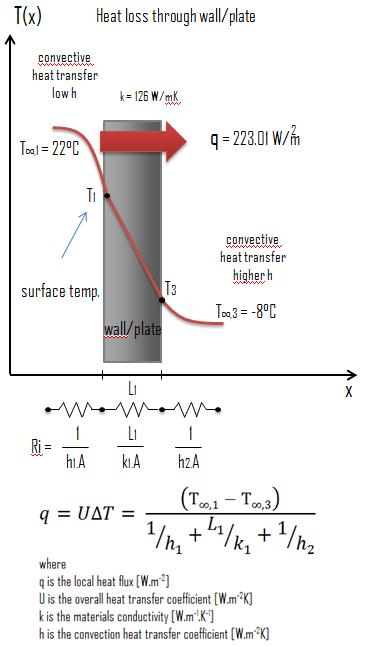
Calcule a taxa de fluxo de calor através de uma parede de 3 m x 10 m de área (A = 30 m²). A parede tem 15 cm de espessura (L₁) e é feita de liga TZM com condutividade térmica de k₁ = 126 W/mK (isolante térmico ruim). Suponha que as temperaturas interna e externa  sejam 22 °C e -8 °C, e os coeficientes de transferência de calor por convecção nos lados interno e externo sejam h₁ = 10 W/m²K e h₂ = 30 W/m²K, respectivamente. Note-se que estes coeficientes de convecção dependem especialmente das condições ambientais e interiores (vento, humidade, etc.).

Calcule o fluxo de calor (perda de calor) através desta parede.

Solução:

Como foi escrito, muitos dos processos de transferência de calor envolvem sistemas compostos e até envolvem uma combinação de condução e convecção. Com esses sistemas compostos, muitas vezes é conveniente trabalhar com um coeficiente global de transferência de calor, conhecido como fator U. O fator U é definido por uma expressão análoga à lei de resfriamento de Newton:

O  coeficiente global de transferência de calor está relacionado com a resistência térmica total e depende da geometria do problema.

Assumindo a transferência de calor unidimensional através da parede plana e desconsiderando a radiação, o coeficiente global de transferência de calor pode ser calculado como:

O coeficiente global de transferência de calor é então: U = 1 / (1/10 + 0,15/126 + 1/30) = 7,43 W/m²K

O fluxo de calor pode então ser calculado simplesmente como: q = 7,43 [W/m²K] x 30 [K] = 223,01 W/m²

A perda total de calor através desta parede será: q_perda = q . A = 223,01 [W/m²] x 30 [m²] = 6690,27 W