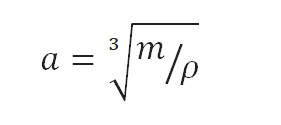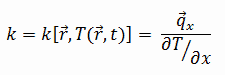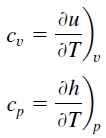Uranium Dioxide – Density – Melting Point – Thermal Conductivity

About Uranium Dioxide

Uranium Dioxide is a ceramic refractory uranium compound, in many cases used as a nuclear fuel. Most of LWRs use the uranium fuel, which is in the form of uranium dioxide (chemically UO2). Uranium dioxide is a black semiconducting solid with very low thermal conductivity. On the other hand the uranium dioxide has very high melting point and has well known behavior. Uranium dioxide has significantly lower density than uranium in the metal form. Uranium dioxide has a density of 10.97 g/cm3, but this value may vary with fuel burnup, because at low burnup densification of pellets can occurs and at higher burnup swelling occurs.

Summary

Name	Uranium Dioxide
Phase at STP	solid
Density	10970 kg/m3
Ultimate Tensile Strength	N/A
Yield Strength	N/A
Young’s Modulus of Elasticity	N/A
Brinell Hardness	N/A
Melting Point	2847 °C
Thermal Conductivity	8.68 W/mK
Heat Capacity	235 J/g K
Price	60 $/kg

Density of Uranium Dioxide

Typical densities of various substances are at atmospheric pressure. Density is defined as the mass per unit volume. It is an intensive property, which is mathematically defined as mass divided by volume:  ρ = m/V

In words, the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance. The standard SI unit is kilograms per cubic meter (kg/m³). The Standard English unit is pounds mass per cubic foot (lbm/ft³).

Density of Uranium Dioxide is 10970 kg/m³.

 

Example: Density

Calculate the height of a cube made of Uranium Dioxide, which weighs one metric ton.

Solution:

Density is defined as the mass per unit volume. It is mathematically defined as mass divided by volume: ρ = m/V

As the volume of a cube is the third power of its sides (V = a³), the height of this cube can be calculated:

The height of this cube is then a = 0.45 m.

Thermal Properties of Uranium Dioxide

Uranium Dioxide – Melting Point

Melting point of Uranium Dioxide is 2847 °C.

Note that, these points are associated with the standard atmospheric pressure. In general, melting is a phase change of a substance from the solid to the liquid phase. The melting point of a substance is the temperature at which this phase change occurs. The melting point also defines a condition in which the solid and liquid can exist in equilibrium. For various chemical compounds and alloys, it is difficult to define the melting point, since they are usually a mixture of various chemical elements.

Uranium Dioxide – Thermal Conductivity

Thermal conductivity of Uranium Dioxide is 8.68 W/(m·K).

The heat transfer characteristics of a solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It is a measure of a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies for all matter, regardless of its state (solid, liquid, or gas), therefore, it is also defined for liquids and gases.

The thermal conductivity of most liquids and solids varies with temperature. For vapors, it also depends upon pressure. In general:

Most materials are very nearly homogeneous, therefore we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.

Uranium Dioxide – Specific Heat

Specific heat of Uranium Dioxide is 235 J/g K.

Specific heat, or specific heat capacity, is a property related to internal energy that is very important in thermodynamics. The intensive properties c_v and c_p are defined for pure, simple compressible substances as partial derivatives of the internal energy u(T, v) and enthalpy h(T, p), respectively:

where the subscripts v and p denote the variables held fixed during differentiation. The properties c_v and c_p are referred to as specific heats (or heat capacities) because under certain special conditions they relate the temperature change of a system to the amount of energy added by heat transfer. Their SI units are J/kg K or J/mol K.

 

Example: Heat transfer calculation

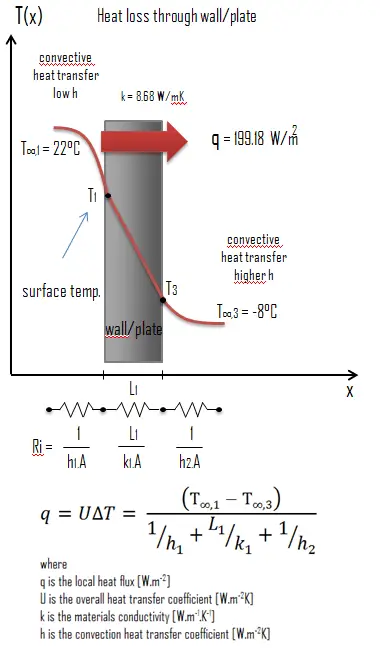Thermal conductivity is defined as the amount of heat (in watts) transferred through a square area of material of given thickness (in metres) due to a difference in temperature. The lower the thermal conductivity of the material the greater the material’s ability to resist heat transfer.

Calculate the rate of heat flux through a wall 3 m x 10 m in area (A = 30 m²). The wall is 15 cm thick (L₁) and it is made of Uranium Dioxide with the thermal conductivity of k₁ = 8.68 W/m.K (poor thermal insulator). Assume that, the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h₁ = 10 W/m²K and h₂ = 30 W/m²K, respectively. Note that, these convection coefficients strongly depend especially on ambient and interior conditions (wind, humidity, etc.).

Calculate the heat flux (heat loss) through this wall.

Solution:

As was written, many of the heat transfer processes involve composite systems and even involve a combination of both conduction and convection. With these composite systems, it is often convenient to work with an overall heat transfer coefficient, known as a U-factor. The U-factor is defined by an expression analogous to Newton’s law of cooling:

The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem.

Assuming one-dimensional heat transfer through the plane wall and disregarding radiation, the overall heat transfer coefficient can be calculated as:

 

The overall heat transfer coefficient is then: U = 1 / (1/10 + 0.15/8.68 + 1/30) = 6.64 W/m²K

The heat flux can be then calculated simply as: q = 6.64 [W/m²K] x 30 [K] = 199.18 W/m²

The total heat loss through this wall will be: q_loss = q . A = 199.18 [W/m²] x 30 [m²] = 5975.52 W