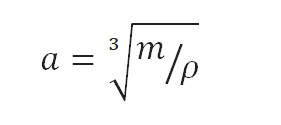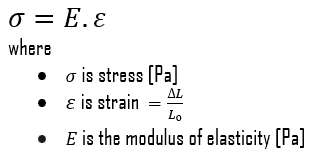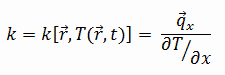Zirconium-Tin Alloy – Density – Strength – Hardness – Melting Point

About Zirconium-Tin Alloy

Zirconium alloys, in which tin is the basic alloying element, provides improvement of their mechanical properties, have a wide distribution in the USA. A common subgroup has the trade mark Zircaloy. In case of zirconium-tin alloys, the decrease of corrosion resistance in water and steam is taken place that resulted in the need for additional alloying.

Zirconium alloys with niobium are used as claddings of fuel elements of VVER and RBMK reactors. These alloys are the basis material of assembly channel of RBMK reactor. The Zr + 1% Nb alloy of type N-1 E-110 is used for fuel element claddings, the Zr + 2.5% Nb alloy of type E-125 is applied for tubes of assembly channels.

Summary

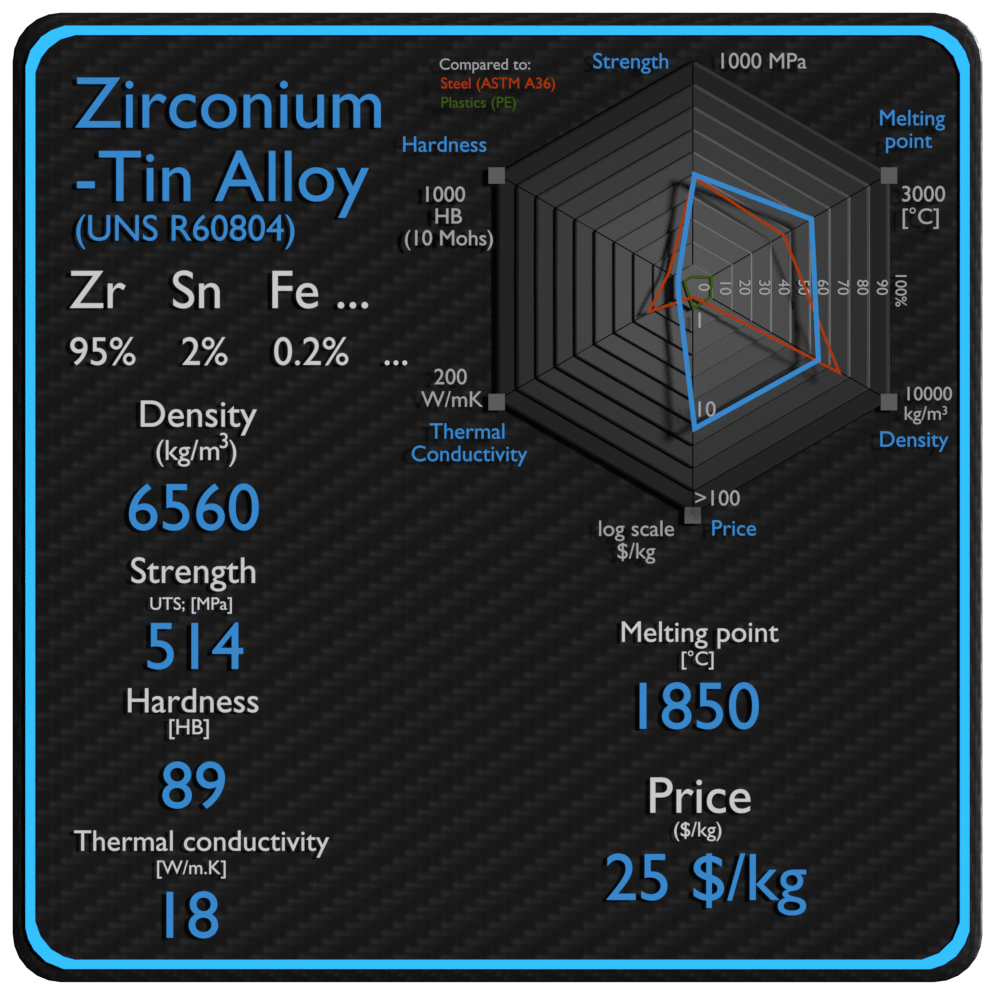
Name	Zirconium-Tin Alloy
Phase at STP	solid
Density	6560 kg/m3
Ultimate Tensile Strength	514 MPa
Yield Strength	381 MPa
Young’s Modulus of Elasticity	99 GPa
Brinell Hardness	89 BHN
Melting Point	1850 °C
Thermal Conductivity	18 W/mK
Heat Capacity	285 J/g K
Price	25 $/kg

Density of Zirconium-Tin Alloy

Typical densities of various substances are at atmospheric pressure. Density is defined as the mass per unit volume. It is an intensive property, which is mathematically defined as mass divided by volume:  ρ = m/V

In words, the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance. The standard SI unit is kilograms per cubic meter (kg/m³). The Standard English unit is pounds mass per cubic foot (lbm/ft³).

Density of Zirconium-Tin Alloy is 6560 kg/m³.

 

Example: Density

Calculate the height of a cube made of Zirconium-Tin Alloy, which weighs one metric ton.

Solution:

Density is defined as the mass per unit volume. It is mathematically defined as mass divided by volume: ρ = m/V

As the volume of a cube is the third power of its sides (V = a³), the height of this cube can be calculated:

The height of this cube is then a = 0.534 m.

Mechanical Properties of Zirconium-Tin Alloy

Strength of Zirconium-Tin Alloy

In mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. Strength of materials basically considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. Strength of a material is its ability to withstand this applied load without failure or plastic deformation.

Ultimate Tensile Strength

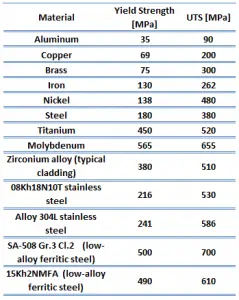
Ultimate tensile strength of Zirconium-Tin Alloy is about 514 MPa.

The ultimate tensile strength is the maximum on the engineering stress-strain curve. This corresponds to the maximum stress that can be sustained by a structure in tension. Ultimate tensile strength is often shortened to “tensile strength” or even to “the ultimate.”  If this stress is applied and maintained, fracture will result. Often, this value is significantly more than the yield stress (as much as 50 to 60 percent more than the yield for some types of metals). When a ductile material reaches its ultimate strength, it experiences necking where the cross-sectional area reduces locally. The stress-strain curve contains no higher stress than the ultimate strength. Even though deformations can continue to increase, the stress usually decreases after the ultimate strength has been achieved. It is an intensive property; therefore its value does not depend on the size of the test specimen. However, it is dependent on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material. Ultimate tensile strengths vary from 50 MPa for an aluminum to as high as 3000 MPa for very high-strength steels.

Yield Strength

Yield strength of Zirconium-Tin Alloy is about 381 MPa.

The yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning plastic behavior. Yield strength or yield stress is the material property defined as the stress at which a material begins to deform plastically whereas yield point is the point where nonlinear (elastic + plastic) deformation begins. Prior to the yield point, the material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible. Some steels and other materials exhibit a behaviour termed a yield point phenomenon. Yield strengths vary from 35 MPa for a low-strength aluminum to greater than 1400 MPa for very high-strength steels.

Young’s Modulus of Elasticity

Young’s modulus of elasticity of Zirconium-Tin Alloy is about 99 GPa.

The Young’s modulus of elasticity is the elastic modulus for tensile and compressive stress in the linear elasticity regime of a uniaxial deformation and is usually assessed by tensile tests. Up to a limiting stress, a body will be able to recover its dimensions on removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position. All the atoms are displaced the same amount and still maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions and no permanent deformation occurs. According to the Hooke’s law, the stress is proportional to the strain (in the elastic region), and the slope is Young’s modulus. Young’s modulus is equal to the longitudinal stress divided by the strain.

Hardness of Zirconium-Tin Alloy

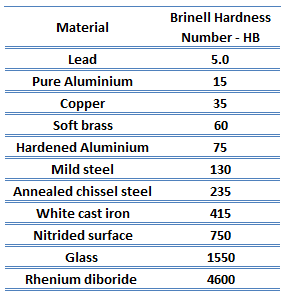
Rockwell hardness of Zirconium-Tin Alloy is approximately 89 HRB.

Rockwell hardness test is one of the most common indentation hardness tests, that has been developed for hardness testing. In contrast to Brinell test, the Rockwell tester measures the depth of penetration of an indenter under a large load (major load) compared to the penetration made by a preload (minor load). The minor load establishes the zero position. The major load is applied, then removed while still maintaining the minor load. The difference between depth of penetration before and after application of the major load is used to calculate the Rockwell hardness number. That is, the penetration depth and hardness are inversely proportional. The chief advantage of Rockwell hardness is its ability to display hardness values directly. The result is a dimensionless number noted as HRA, HRB, HRC, etc., where the last letter is the respective Rockwell scale.

The Rockwell C test is performed with a Brale penetrator (120°diamond cone) and a major load of 150kg.

 

Example: Strength

Assume a plastic rod, which is made of Zirconium-Tin Alloy. This plastic rod has a cross-sectional area of 1 cm². Calculate the tensile force needed to achieve the ultimate tensile strength for this material, which is: UTS = 514 MPa.

Solution:

Stress (σ) can be equated to the load per unit area or the force (F) applied per cross-sectional area (A) perpendicular to the force as:

therefore, the tensile force needed to achieve the ultimate tensile strength is:

F = UTS x A = 514 x 10⁶ x 0.0001 = 51 400 N

Thermal Properties of Zirconium-Tin Alloy

Thermal properties of materials refer to the response of materials to changes in their temperature and to the application of heat. As a solid absorbs energy in the form of heat, its temperature rises and its dimensions increase. But different materials react to the application of heat differently.

Heat capacity, thermal expansion, and thermal conductivity are properties that are often critical in the practical use of solids.

Melting Point of Zirconium-Tin Alloy

Melting point of Zirconium-Tin Alloy is around 1850°C.

In general, melting is a phase change of a substance from the solid to the liquid phase. The melting point of a substance is the temperature at which this phase change occurs. The melting point also defines a condition in which the solid and liquid can exist in equilibrium.

Thermal Conductivity of Zirconium-Tin Alloy

Zirconium alloys have lower thermal conductivity (about 18 W/m.K) than pure zirconium metal (about 22 W/m.K).

The heat transfer characteristics of a solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It is a measure of a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies for all matter, regardless of its state (solid, liquid, or gas), therefore, it is also defined for liquids and gases.

The thermal conductivity of most liquids and solids varies with temperature. For vapors, it also depends upon pressure. In general:

Most materials are very nearly homogeneous, therefore we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.

 

Example: Heat transfer calculation

Thermal conductivity is defined as the amount of heat (in watts) transferred through a square area of material of given thickness (in metres) due to a difference in temperature. The lower the thermal conductivity of the material the greater the material’s ability to resist heat transfer.

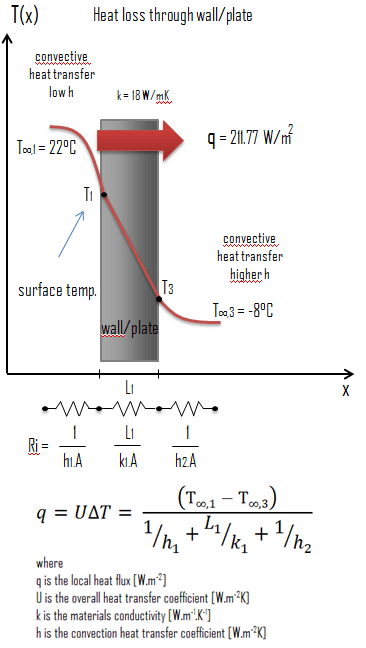
Calculate the rate of heat flux through a wall 3 m x 10 m in area (A = 30 m²). The wall is 15 cm thick (L₁) and it is made of Zirconium-Tin Alloy with the thermal conductivity of k₁ = 18 W/m.K (poor thermal insulator). Assume that, the indoor and the outdoor temperatures are 22°C and -8°C, and the convection heat transfer coefficients on the inner and the outer sides are h₁ = 10 W/m²K and h₂ = 30 W/m²K, respectively. Note that, these convection coefficients strongly depend especially on ambient and interior conditions (wind, humidity, etc.).

Calculate the heat flux (heat loss) through this wall.

Solution:

As was written, many of the heat transfer processes involve composite systems and even involve a combination of both conduction and convection. With these composite systems, it is often convenient to work with an overall heat transfer coefficient, known as a U-factor. The U-factor is defined by an expression analogous to Newton’s law of cooling:

The overall heat transfer coefficient is related to the total thermal resistance and depends on the geometry of the problem.

Assuming one-dimensional heat transfer through the plane wall and disregarding radiation, the overall heat transfer coefficient can be calculated as:

 

The overall heat transfer coefficient is then: U = 1 / (1/10 + 0.15/18 + 1/30) = 7.06 W/m²K

The heat flux can be then calculated simply as: q = 7.06 [W/m²K] x 30 [K] = 211.77 W/m²

The total heat loss through this wall will be: q_loss = q . A = 211.77 [W/m²] x 30 [m²] = 6352.94 W