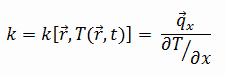——
0.598 W/(m.K)
——
0.025 W/(m.K)
——
2.22 W/(m.K)
——
1.05 W/(m.K)
——
30 W/(m.K)
——
200 W/(m.K)
——
100 W/(m.K)
——
0.5 W/(m.K)
——
0.2 W/(m.K)
——
0.0166 W/(m.K)
——
1.31 W/(m.K)
——
1.5 W/(m.K)
——
110 W/(m.K)
——
1000 W/(m.K)
——
4000 W/(m.K)
——
0.3 W/(m.K)
——
0.2 W/(m.K)
——
0.024 W/(m.K)
——
0.25 W/(m.K)
——
1.3 W/(m.K)
——
116 W/(m.K)
——
140 W/(m.K)
——
18 W/(m.K)
——
20 W/(m.K)
——
50 W/(m.K)
——
53 W/(m.K)
——
126 W/(m.K)
——
6.5 W/(m.K)
——
394 W/(m.K)
——
40 W/(m.K)
——
113 W/(m.K)
——
40 W/(m.K)
——
8.68 W/(m.K)
——
0.12 W/(m.K)
——
0.2 W/(m.K)
——
0.042 W/(m.K)
——
0.5 W/(m.K)
——
3.2 W/(m.K)
——
22 W/(m.K)
——
150 W/(m.K)
——
18 W/(m.K)
——
24 W/(m.K)
——
50 W/(m.K)
——
15-30 W/(m.K)
——
70 W/(m.K)
——
10.2 W/(m.K)
——
120 W/(m.K)
——
59 W/(m.K)
——
50 W/(m.K)
——
7 W/(m.K)
——
0.04 W/(m.K)
——
0.2 W/(m.K)
——
0.5 W/(m.K)
——
0.034 W/(m.K)
——
0.3 W/(m.K)
——
3 W/(m.K)
——
6.7 W/(m.K)
——
190 W/(m.K)
——
41 W/(m.K)
——
19 W/(m.K)
——
26 W/(m.K)
——
36 W/(m.K)
——
70 W/(m.K)
——
14.8 W/(m.K)
——
75 W/(m.K)
——
115 W/(m.K)
——
23 W/(m.K)
——
0.15 W/(m.K)
——
0.2 W/(m.K)
——
0.2 W/(m.K)
——
0.75 W/(m.K)
——
0.017 W/(m.K)
——
0.03 W/(m.K)
——
0.01 W/(m.K)
——
300 W/(m.K)
——
320 W/(m.K)
——
250 W/(m.K)
——
18 W/(m.K)
——
41 W/(m.K)
——
40 W/(m.K)
——
170 W/(m.K)
——
12 W/(m.K)
——
21.2 W/(m.K)
——
40 W/(m.K)
——
16.5 W/(m.K)
——
0.17 W/(m.K)
——
0.12 W/(m.K)
——
0.16 W/(m.K)
——
0.13 W/(m.K)
——
0.024 W/(m.K)
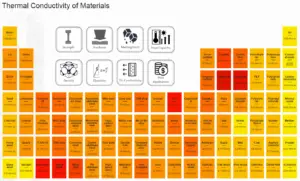
Thermal Conductivity of Materials
The heat transfer characteristics of a solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It is a measure of a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies for all matter, regardless of its state (solid, liquid, or gas), therefore, it is also defined for liquids and gases.
The thermal conductivity of most liquids and solids varies with temperature. For vapors, it also depends upon pressure. In general:
Most materials are very nearly homogeneous, therefore we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.
Thermal Conductivity of Metals
- the migration of free electrons
- lattice vibrational waves (phonons)
When electrons and phonons carry thermal energy leading to conduction heat transfer in a solid, the thermal conductivity may be expressed as:
k = ke + kph
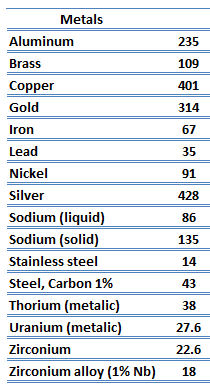 Metals are solids and as such they possess crystalline structure where the ions (nuclei with their surrounding shells of core electrons) occupy translationally equivalent positions in the crystal lattice. Metals in general have high electrical conductivity, high thermal conductivity, and high density. Accordingly, transport of thermal energy may be due to two effects:
Metals are solids and as such they possess crystalline structure where the ions (nuclei with their surrounding shells of core electrons) occupy translationally equivalent positions in the crystal lattice. Metals in general have high electrical conductivity, high thermal conductivity, and high density. Accordingly, transport of thermal energy may be due to two effects:
- the migration of free electrons
- lattice vibrational waves (phonons).
When electrons and phonons carry thermal energy leading to conduction heat transfer in a solid, the thermal conductivity may be expressed as:
k = ke + kph
The unique feature of metals as far as their structure is concerned is the presence of charge carriers, specifically electrons. The electrical and thermal conductivities of metals originate from the fact that their outer electrons are delocalized. Their contribution to the thermal conductivity is referred to as the electronic thermal conductivity, ke. In fact, in pure metals such as gold, silver, copper, and aluminum, the heat current associated with the flow of electrons by far exceeds a small contribution due to the flow of phonons. In contrast, for alloys, the contribution of kph to k is no longer negligible.
Thermal Conductivity of Nonmetals
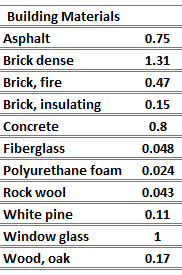 For nonmetallic solids, k is determined primarily by kph, which increases as the frequency of interactions between the atoms and the lattice decreases. In fact, lattice thermal conduction is the dominant thermal conduction mechanism in nonmetals, if not the only one. In solids, atoms vibrate about their equilibrium positions (crystal lattice). The vibrations of atoms are not independent of each other, but are rather strongly coupled with neighboring atoms. The regularity of the lattice arrangement has an important effect on kph, with crystalline (well-ordered) materials like quartz having a higher thermal conductivity than amorphous materials like glass. At sufficiently high temperatures kph ∝ 1/T.
For nonmetallic solids, k is determined primarily by kph, which increases as the frequency of interactions between the atoms and the lattice decreases. In fact, lattice thermal conduction is the dominant thermal conduction mechanism in nonmetals, if not the only one. In solids, atoms vibrate about their equilibrium positions (crystal lattice). The vibrations of atoms are not independent of each other, but are rather strongly coupled with neighboring atoms. The regularity of the lattice arrangement has an important effect on kph, with crystalline (well-ordered) materials like quartz having a higher thermal conductivity than amorphous materials like glass. At sufficiently high temperatures kph ∝ 1/T.
The quanta of the crystal vibrational field are referred to as ‘‘phonons.’’ A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids. Phonons play a major role in many of the physical properties of condensed matter, like thermal conductivity and electrical conductivity. In fact, for crystalline, nonmetallic solids such as diamond, kph can be quite large, exceeding values of k associated with good conductors, such as aluminum. In particular, diamond has the highest hardness and thermal conductivity (k = 1000 W/m.K) of any bulk material.
Thermal Conductivity of Liquids and Gases
In physics, a fluid is a substance that continually deforms (flows) under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids. Because the intermolecular spacing is much larger and the motion of the molecules is more random for the fluid state than for the solid state, thermal energy transport is less effective. The thermal conductivity of gases and liquids is therefore generally smaller than that of solids. In liquids, the thermal conduction is caused by atomic or molecular diffusion. In gases, the thermal conduction is caused by diffusion of molecules from higher energy level to the lower level.
Thermal Conductivity of Gases
 The effect of temperature, pressure, and chemical species on the thermal conductivity of a gas may be explained in terms of the kinetic theory of gases. Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials (e.g.polystyrene) function simply by having a large number of gas-filled pockets which prevent large-scale convection. Alternation of gas pocket and solid material causes that the heat must be transferred through many interfaces causing rapid decrease in heat transfer coefficient.
The effect of temperature, pressure, and chemical species on the thermal conductivity of a gas may be explained in terms of the kinetic theory of gases. Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials (e.g.polystyrene) function simply by having a large number of gas-filled pockets which prevent large-scale convection. Alternation of gas pocket and solid material causes that the heat must be transferred through many interfaces causing rapid decrease in heat transfer coefficient.
The thermal conductivity of gases is directly proportional to the density of the gas, the mean molecular speed, and especially to the mean free path of molecule. The mean free path also depends on the diameter of the molecule, with larger molecules more likely to experience collisions than small molecules, which is the average distance traveled by an energy carrier (a molecule) before experiencing a collision. Light gases, such as hydrogen and helium typically have high thermal conductivity. Dense gases such as xenon and dichlorodifluoromethane have low thermal conductivity.
In general, the thermal conductivity of gases increases with increasing temperature.
Thermal Conductivity of Liquids
As was written, in liquids, the thermal conduction is caused by atomic or molecular diffusion, but physical mechanisms for explaining the thermal conductivity of liquids are not well understood. Liquids tend to have better thermal conductivity than gases, and the ability to flow makes a liquid suitable for removing excess heat from mechanical components. The heat can be removed by channeling the liquid through a heat exchanger. The coolants used in nuclear reactors include water or liquid metals, such as sodium or lead.
The thermal conductivity of nonmetallic liquids generally decreases with increasing temperature.